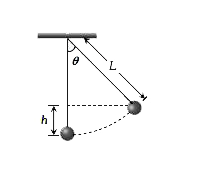
A simple pendulum with a bob of mass m and a conducting wire of length L, swings under gravity with an angular amplitude 2θ. If the horizontal component of the earth's magnetic field perpendicular to the plane of motion of the pendulum is B, then the maximum emf induced across the pendulum is
2BLsin(θ2)(gL)1/2
BLsin(θ2)(gL)
BLsin(θ2)(gL)3/2
BLsin(θ2)(gL)2
The correct Answer is:A
h=L(1−cosθ)
v2=2gh
⇒v2=2gL(1−cosθ)
⇒v2=2gL(2sin2θ2)
∴v=2√gLsinθ/2
emf e = BvL = 2B(√gLsinθ/2)L
= 2BLsin(θ/2)(gL)12.
Similar Questions
A conductor of length 2.0m is falling freely under gravity from a height of 15 m so that it cuts the magnetic lines of force of the horizontal component of Earth's magnetic field of strength 0.3 gauss. Calculate the emf induced across the conductor.
View SolutionA simple pendulum with a bob of mass m swings with an angular amplitude of 40∘. When its angular displacement is 20∘, the tension in the string is greater than mgcos20∘
View Solution
Knowledge Check
A simple pendulum with bob of mass m and conducting wire of length L swings under gravity through an angle 2θ. The earth’s magnetic field component in the direction perpendicular to swing is B . Maximum potential difference induced across the pendulum is
 A2BLsin(θ2)(gL)1/2BBLsin(θ2)(gL)CBLsin(θ2)(gL)3/2DBLsin(θ2)(gL)2
A2BLsin(θ2)(gL)1/2BBLsin(θ2)(gL)CBLsin(θ2)(gL)3/2DBLsin(θ2)(gL)2A simple pendulum with bob of mass m and conducting wire of length L swings under gravity through an angle 2θ . The earth's magnetic field component in the direction perpendicular to swing is B . Maximum potential difference induced across the pendulum is
 A2BLsin(θ2)(gL)1/2BBLsin(θ2)(gL)CBLsin(θ2)(gL)3/2DBLsin(θ2)(gL)2
A2BLsin(θ2)(gL)1/2BBLsin(θ2)(gL)CBLsin(θ2)(gL)3/2DBLsin(θ2)(gL)2A simple pendulum with charge bob is oscillating as shown in the figure. Time period of oscillation is T and angular ampliltude is θ. If a uniform magnetic field perpendicular to the plane of oscillation is switched on, then
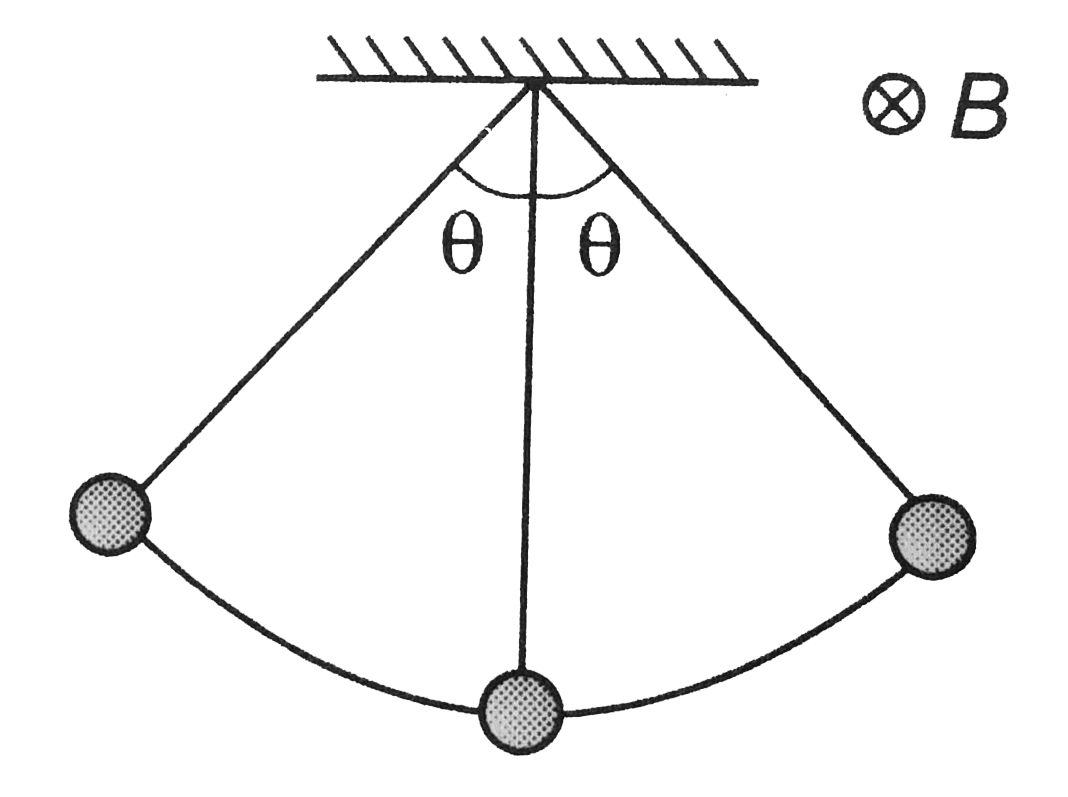 AT will decrease but θ will remain constantBT wil remainconstant but θ will decreaseCBoth T and θ will remain the sameDBoth T and theta will decrease
AT will decrease but θ will remain constantBT wil remainconstant but θ will decreaseCBoth T and θ will remain the sameDBoth T and theta will decrease
A simple pendulum of length 'l' carries a bob of mass 'm'. If the breaking strength of the string is 3mg, the maximum angular amplitude from the vertical can be
View SolutionA simple pendulum length l made of conducting material swings with small amplitude θ0 in a uniform magnetic field of magnetic induction B. Plot the voltage induced in the pendulum if the magnetic field is perpendicular to the plane of oscillation. At t = 0, the string is vertical.
View SolutionA simple pendulum of length 1 m with a bob of mass m swings with an angular amplitude 30∘. Then (g=9.8m/s2
View SolutionA simple pendulum of length 1 m with a bob of mass m swings with an angular amplitude 30°. Then (g = 9.8 ms−2)
View SolutionA simple pendulum has a bob of mass m and swings with an angular amplitude ϕ. The tension in thread is T. At a certain time the string makes an angle θ with the vertical (θ≤ϕ)
View Solution
