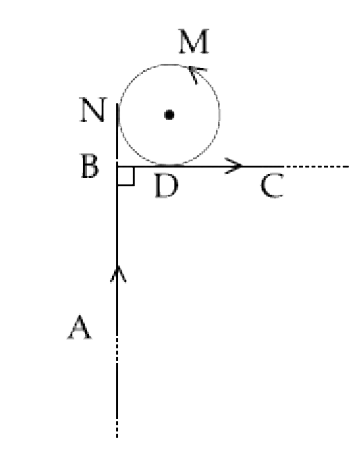
A very long wire ABDMNDC is shown in figure carrying current I. AB and BC parts are straight, long and at right angle. At D wire forms a circular turn DMND of radius R. AB, BC parts are tangential to circular turn at N and D. Magnetic field at the centre of circle is :
μ0I2πR(π+1√2)
μ0I2R
μ0I2πR(π−1√2)
μ0I2πR(π+1)
The correct Answer is:A

→B0=(→B0)A+(→B0)B+(→B0)C
μ0I4πR[sin90∘−sin45∘]⊗+μ0I2R⊙+μ0I4πR(sin45∘−sin90∘)⊙
μ0I4πR[1−1√2]+μ0I2R+μ0I4πR[1√2+1]⊙
μ0I4πR[−1+1√2+2π+1√2+1]⊙=μ0I4πR[√2+2π]⊙μ0I2πR[1√2+π]⊙
Similar Questions
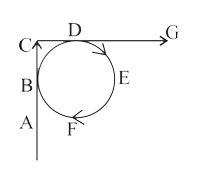
A very long wire ABCDEFBDG is shown in figure carrying current I. AC and CG parts are straight, long and at right angle. At D wire forms a circular turn DEFBD of radius R. AC, CG parts are tangential to circular turn at B and D. Magnetic field at the centre of circle is:
View SolutionA long wire having a semi-circular loop of radius r carries a current I, as shown in Fig. Find the magnetic field due to entire wire.

View Solution
Knowledge Check
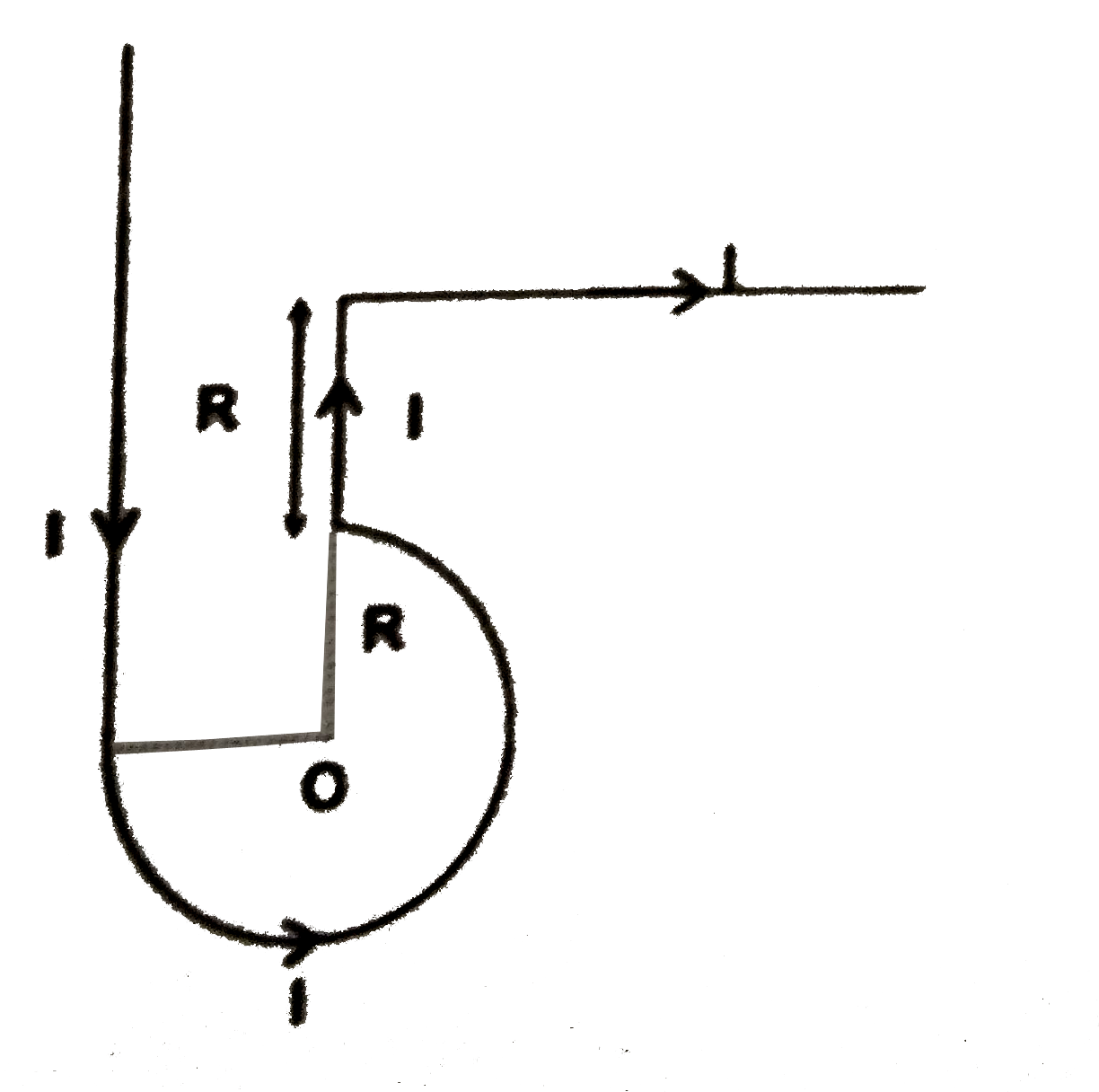
A conducting wire carrying a current I is bent into the shape as shown. The net magnetic field at the centre O of the circular arc of radius RAμ0l2R(1+3ππ)Bμ0l4R(1+3ππ)Cμ0l8R(1+3ππ)Dμ0l8R(2+3ππ)A long wire bent as shown in fig. carries current I. If the radius of the semicircular portion is a, the magnetic field at centre C is
 Aμ0I4aBμ0I4πa√π2+4Cμ0I4a+μ0I4πaDμ0I4πa√(π2−4)
Aμ0I4aBμ0I4πa√π2+4Cμ0I4a+μ0I4πaDμ0I4πa√(π2−4)A circular coil of n turns and radius r carries a current I. The magnetic field at the center is
Aμ0nIrBμ0nI2rC2μ0nIrDμ0nI4r
A0.5 m long conducting wire is bent in form of a circle, Calculate the magnetic field at the centre if wire carries a current of 5 A.
View SolutionA long wire carries a steady curent . It is bent into a circle of one turn and the magnetic field at the centre of the coil is B. It is then bent into a circular loop of n turns. The magnetic field at the centre of the coil will be
View SolutionA long straight conductor carrying a current i is bent to form an almost complete circular loop of radius r on it. The magnetic field at the centre of the loop
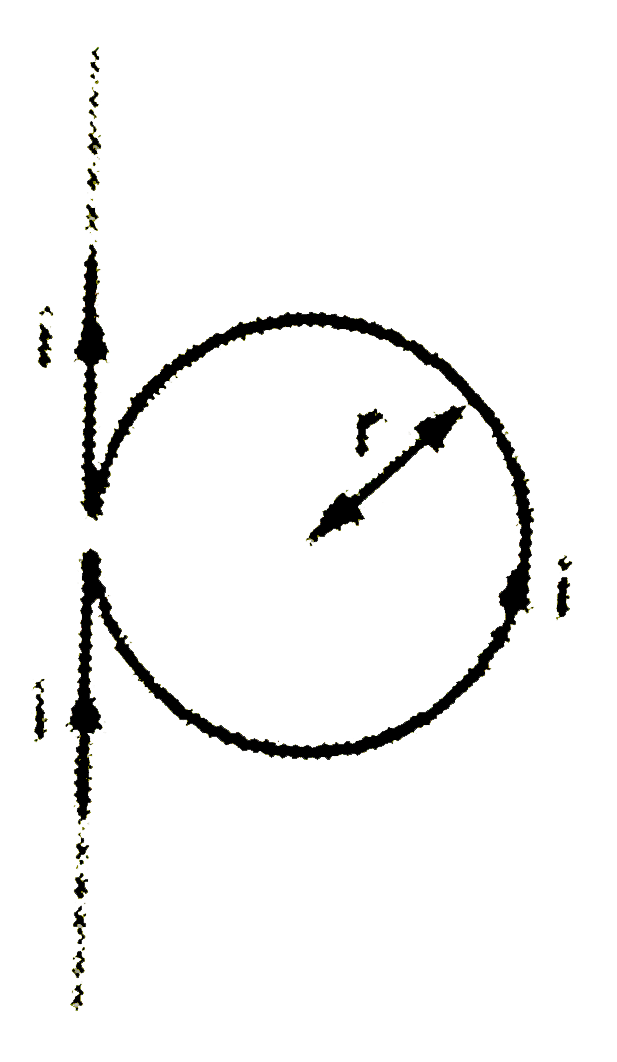
View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is
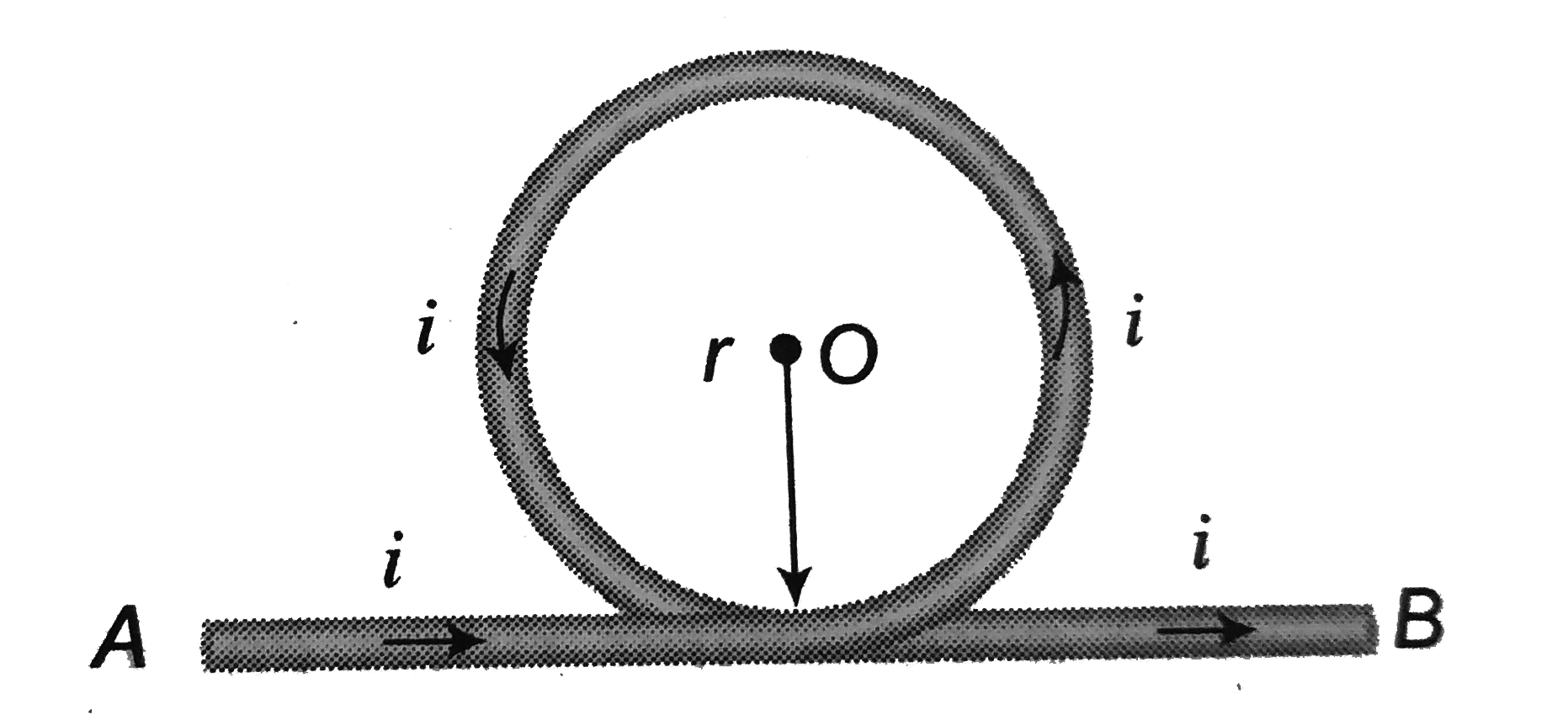
View SolutionA long wire carrying a steady current is bent into a circular loop of one turn. The magnetic field at the centre of the loop is B. It is then bent into a circular coil of n turns. The magnetic field at the centre of this coil of n turns will be
View Solution