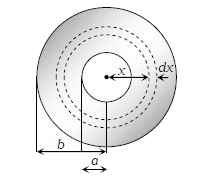
A coil having turns is would tightly in the form of a spiral with inner and outer radii a and respectively. When a current passes through the coil, the magnetic field at the centre is.
The correct Answer is:C
Number of turns per unit length
Number of turns in ring
Similar Questions
A coil having N turns is wound tightly in the form of a spiral with inner and outer radii 'a' and 'b' respectively. Find the magnetic field at centre, when a current I passes through coil:
View SolutionA flat coil, in the shape of a spiral, has a large number of turns N. The turns are wound tightly and the inner and outer radii of the coil are a and b respectively. A uniform external magnetic field (B) is applied perpendicular to the plane of the coil. Find the emf induced in the coil when the field is made to change at a rate dBdt.

View Solution
Knowledge Check
A coil having N turns is would tightly in the form of a spiral with inner and outer radii a and b respectively. When a current I passes through the coil, the magnetic field at the centre is.
Aμ0NIb−aBμ0NI2π(b−a)Cμ0NI2(b−a)InbaDμ0NIb−aInbaA coil having N turns is wound tightly in the form of a spiral with inner and outer radii a and b respectively. A current I passes through the coil. The magnetic moment of the spriral is
AM=μ0NI3b3−a3(b−a)3BM=πNI3(b−a)3b3−a3CM=πNI3(b3−a3)(b−a)3DM=μ0NI3(b−a)3b3−a3A coil of n number of tums is wound tightly in the form of a spiral with inner and outer radii a and b respectively. When a current of strength / is passed through the coil, the magnetic field at its centre is
Aμ0nl(b−a)logebaBμ0nl2(b−a)C2μ0nlbDμ0nl2(b−a)logeba
A toroidal coil has 3000 turns. The inner and outer radii are 10 cm and 12 cm respectively. If current flowing is 5 A, then the magnetic field inside the toroid will be
View SolutionA long insulated copper wire is closely wound as a spiral of N turns. The spiral has inner radius a and outer radius b. The spiral lies in the xy-plane and a steady current I flows through the wire. Thez-component of the magetic field at the centre of the spiral is

View SolutionA current passing through a circular coil of two turns produces a magnetic field B as its centr. The coil is then rewound so as to have four turns and the same current is passed through it. The magnetic field at its centre now is
View SolutionA circular coil carrying a certain, current produces a magnetic field B0 at its centre. The coil is now rewound so a to have 3 turns and the same currents is passed through it. The new magnetic field at the centre is
View SolutionA circular coil carrying a certain current produces a megnetic field Bo at its centre. The coil is now rewound so as to have 3 turns and the same current is passed through it. The new magnetic field at the centre is
View Solution