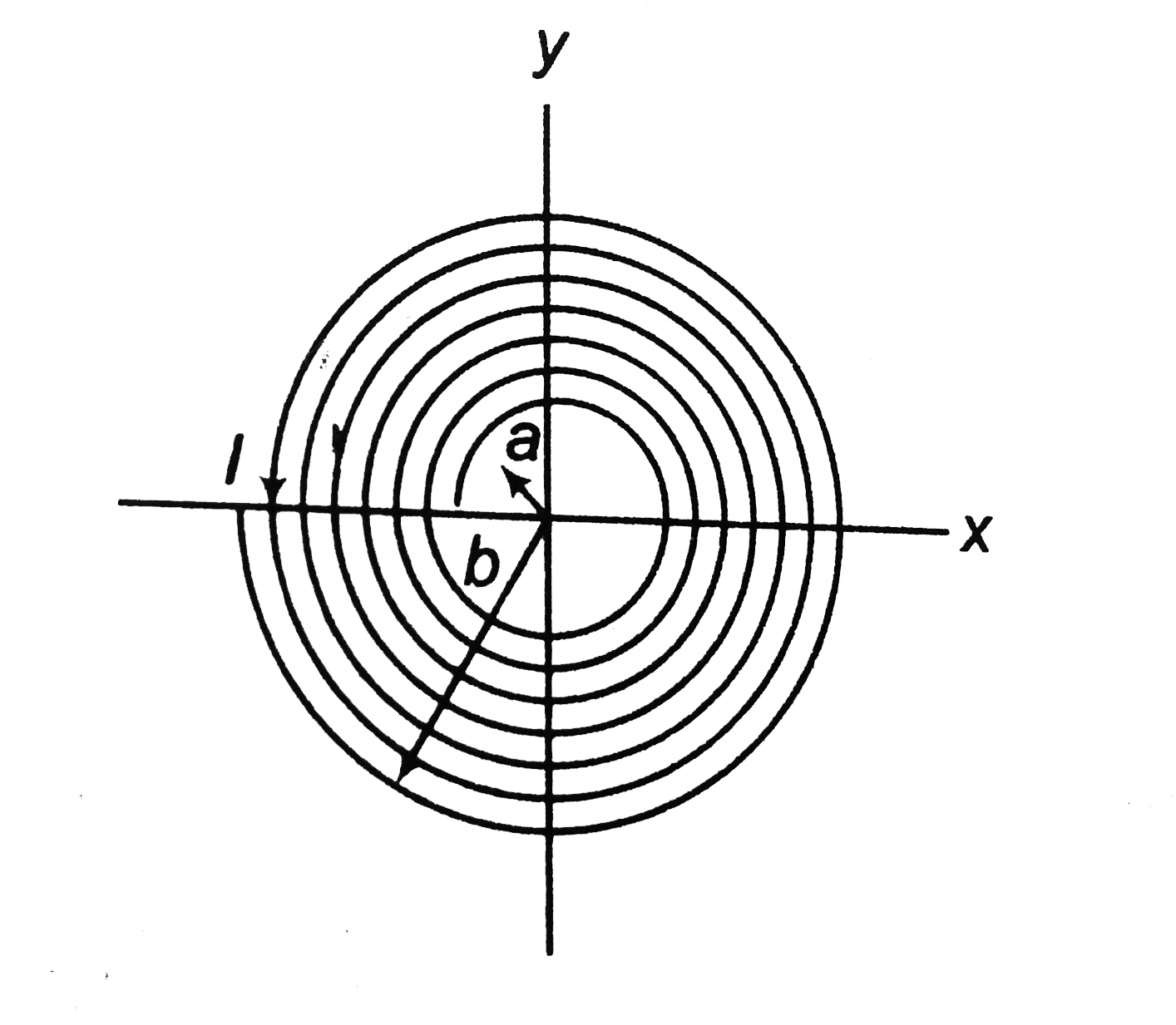
A long insulated copper wire is closely wound as a spiral of N turns. The spiral has inner radius a and outer radius b. The spiral lies in the xy-plane and a steady current I flows through the wire. Thez-component of the magetic field at the centre of the spiral is
μ0NI2(b−a)ln(ba)
μ0NI2(b−a)ln(b+ab−a)
μ0NI2bln(ba)
μ0NI2b(b+ab−a)
The correct Answer is:A
a. If we take a small strip of dr at distance r from centre, then number of turns in this strip would be
dN=(Nb−a)dr
Magnetic field due to this element at the cenntre of the coil will be
dB=(μ0)(dN)I2r=μ0NI(b−a)dr2r
∴B∫r=br=adB=μ0NI2(b−a)ln(ba)
:. current answer is a.
Topper's Solved these Questions
- MAGNETICSBook:DC PANDEYChapter:MAGNETICSExercise:Exercise
Explore 160 Videos
- MAGNETICSBook:DC PANDEYChapter:MAGNETICSExercise:INTRODUCTORY EXERCISE
Explore 1 Video
- MAGNETIC FIELD AND FORCESBook:DC PANDEYChapter:MAGNETIC FIELD AND FORCESExercise:Medical entrance s gallery
Explore 59 Videos
- MAGNETISM AND MATTERBook:DC PANDEYChapter:MAGNETISM AND MATTERExercise:Medical gallery
Explore 1 Video
Similar Questions
The magnetic field at the centre of a tightly wound spiral coil with inner radius R and outer radius 4.5 R with number of turns 22, when current i is flowing through it, is
View SolutionA circular coil 'A' has a radius R and the current flowing through it is I.Another circular coil 'B' has a radius 2R and if 2I is the current flowing through it then the magnetic fields at the centre of the circular coil are in the ratio of
View Solution
Knowledge Check
A long insulated copper wire is closely wound as a spiral of N turns. The spiral has inner radius a and outer radius b. The spiral lies in the xy-plane and a steady current I flows through the wire. Thez-component of the magetic field at the centre of the spiral is
 Aμ0NI2(b−a)ln(ba)Bμ0NI2(b−a)ln(b+ab−a)Cμ0NI2bln(ba)Dμ0NI2bln(b+ab−a)
Aμ0NI2(b−a)ln(ba)Bμ0NI2(b−a)ln(b+ab−a)Cμ0NI2bln(ba)Dμ0NI2bln(b+ab−a)A coil having N turns is would tightly in the form of a spiral with inner and outer radii a and b respectively. When a current I passes through the coil, the magnetic field at the centre is.
Aμ0NIb−aBμ0NI2π(b−a)Cμ0NI2(b−a)InbaDμ0NIb−aInbaA toroid of core of inner radius 0.25 m and outer radius 0.26 m around which 3500 turns of a wire are wound. If the current in the wire is 11 A, then magnetic field inside the core of the toroid is
A3×102TB3×10−2TC3×10−7TD3×107T
A circular coil 'A' has a radius R and the current flowing through it is I.Another circular coil 'B' has a radius 2R and if 21is the current flowing through it then the magnetic fields at the centre of the circular coil are in the ratio of
View SolutionA circular coil 'A' has a radius R and the current flowing through it is I.Another circular coil 'B' has a radius 2R and if 21is the current flowing through it then the magnetic fields at the centre of the circular coil are in the ratio of
View SolutionA coil having N turns is would tightly in the form of a spiral with inner and outer radii a and b respectively. When a current I passes through the coil, the magnetic field at the centre is.
View SolutionA toroid has a core of inner radius 20cm and outer radius 22cm around which 4200 turns of a wire are wound. If the current in the wire is 10A, what is the magnetic field
(a) inside the core of toroid (b) outside the toroid
(c) in the empty space surrounded by toroid?
View SolutionA coil of n number of tums is wound tightly in the form of a spiral with inner and outer radii a and b respectively. When a current of strength / is passed through the coil, the magnetic field at its centre is
View Solution

