A wire bent in the shape of a regular n-polygonal loop carries a steady current I. Let l be the perpendicular distance of a given segment and R be the distance of vertex both from the centre of the loop. The magnitude of the magnetic field at the centre of the loop is given by -
nμ0I2πlsin (π/n)
nμ02πIRsin(π/n)
nμ02πIlcos(π/n)
nμ0I2πRcos(π/n)
The correct Answer is:A
B=μ0I4πl×2sinθ [ where 2θ=2πn]
Similar Questions
Knowledge Check
In the given loop the magnetic field at the centre O is
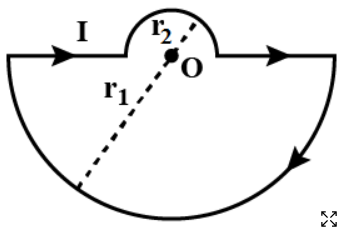 AμI4(r1+r2r1r2) out of the pageBμ0I4(r1+r2r1r2) into the pageCμ0I4(r1−r2r1r2) out of the pageDμ0I4(r1−r2r1r2) into the page
AμI4(r1+r2r1r2) out of the pageBμ0I4(r1+r2r1r2) into the pageCμ0I4(r1−r2r1r2) out of the pageDμ0I4(r1−r2r1r2) into the pageA square loop of side a carries a current I. The magnetic field at the center of the loop is
A2μ0I√2πaBμ0I√2πaC4μ0I√2πaDμ0IπaA wire of length L carrying a current I is bent into a circle. The magnitude of the magnetic field at the centre of the circle is
Aπμ0ILBμ0I2LC2πμ0ILDμ0I2πL
A loop carrying current I has the shape of a regular polygon of n sides. If R is the distance from the centre to any vertex, then the magnitude of the magnetic induction vector →B at the centre of the loop is –
View SolutionAlong wire carries a steady current. It is bent into a circle of one tum and the magnetic field at the centre of the coil is B. It is then bent into a circular loop of N tums. The magnetic field at the centre of the coil will be
View SolutionA symmetric star shaped conducting wire loop is carrying a steady state current I as shown in the figure. The distance between the diametrically opposite vertices of the star is 4a. The magnitude of the magnetic field at the center of the loop is
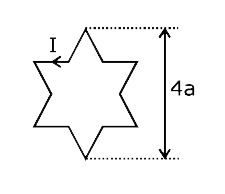
View SolutionA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is
View SolutionA long wire carries a steady curent . It is bent into a circle of one turn and the magnetic field at the centre of the coil is B. It is then bent into a circular loop of n turns. The magnetic field at the centre of the coil will be
View Solution
