A current carrying conductor of length l is bent into two loops one by one. First loop has one turn of wire and the second loop has two turns of wire. Compare the magnetic fields at the centre of the loops
B'=4B
4B'=B
2B'=B
B'=2B
The correct Answer is:A
To solve the problem of comparing the magnetic fields at the center of two loops formed by bending a current-carrying conductor of length L, we will follow these steps:
Step 1: Understanding the Magnetic Field Formula
The magnetic field B at the center of a circular loop carrying current I is given by the formula:
B=nμ0I2a
where:
- n = number of turns in the loop
- μ0 = permeability of free space
- I = current through the wire
- a = radius of the loop
Step 2: Analyze the First Loop
For the first loop:
- It has 1 turn, so n=1.
- The length of the wire used for this loop is L, which corresponds to the circumference of the loop:
2πa=L⟹a=L2π
Now, substituting n and a into the magnetic field formula:
B1=1⋅μ0I2⋅L2π=μ0I⋅πL
Step 3: Analyze the Second Loop
For the second loop:
- It has 2 turns, so n=2.
- The length of the wire used for this loop is still L, which corresponds to the circumference of the two loops combined:
2πa′=L2⟹a′=L4π
Now, substituting n and a′ into the magnetic field formula:
B2=2⋅μ0I2⋅L4π=2⋅μ0I⋅2πL=4μ0I⋅πL
Step 4: Compare the Magnetic Fields
Now we have:
- B1=μ0I⋅πL
- B2=4μ0I⋅πL
To compare B1 and B2:
B1B2=μ0I⋅πL4μ0I⋅πL=14
This implies:
B2=4B1
Conclusion
The magnetic field at the center of the second loop (with two turns) is four times greater than that of the first loop (with one turn).
The magnetic field B at the center of a circular loop carrying current I is given by the formula:
B=nμ0I2a
where:
- n = number of turns in the loop
- μ0 = permeability of free space
- I = current through the wire
- a = radius of the loop
For the first loop:
- It has 1 turn, so n=1.
- The length of the wire used for this loop is L, which corresponds to the circumference of the loop:
2πa=L⟹a=L2π
Now, substituting n and a into the magnetic field formula:
B1=1⋅μ0I2⋅L2π=μ0I⋅πL
For the second loop:
- It has 2 turns, so n=2.
- The length of the wire used for this loop is still L, which corresponds to the circumference of the two loops combined:
2πa′=L2⟹a′=L4π
Now, substituting n and a′ into the magnetic field formula:
B2=2⋅μ0I2⋅L4π=2⋅μ0I⋅2πL=4μ0I⋅πL
Now we have:
- B1=μ0I⋅πL
- B2=4μ0I⋅πL
B1B2=μ0I⋅πL4μ0I⋅πL=14
This implies:
B2=4B1
The magnetic field at the center of the second loop (with two turns) is four times greater than that of the first loop (with one turn).
Topper's Solved these Questions
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEYCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Assertion and reason
20 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEYCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Match the following
4 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEYCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Check point
54 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Subjective
5 Videos
- MAGNETICSBOOK - DC PANDEYCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
Similar Questions
An infinitely long straight conductor is bent into the shape as shown in figure. It carries the current I and radius of the circular loop is a, then the magnetic field at the centre of the loop is ______
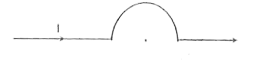
View SolutionA conducting circular loop of radius a is connected to two long, straight wires . The straight wires carry a current I as shown in figure . Find the magnetic field B at the centre of the loop.

View Solution
Knowledge Check
A square loop of side a carries a current I. The magnetic field at the center of the loop is
A2μ0I√2πaBμ0I√2πaC4μ0I√2πaDμ0IπaA square loop of edge 'a' carries a current l. The magnetic field at the centre of loop is
Aμ0l2√2πaB2√2μ0lπaCμ0l√2πaDμ0l√2πaA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is
Aindependent of LBproportional LCinversely proportional to LDlinearly proportional to L
One of the two identical conducting wires of length L is bent in the form of a circular loop and the other one into a circular coil of N identical turns. If the same current passed in both, the ratio of the magnetic field at the central of the loop (BL) to that at the central of the coil (BC), i.e. BLBC will be :
View SolutionA rectangular loop of metallic wire is of length a and breadth b and carries a current i. The magnetic field at the centre of the loop is
View SolutionA star shaped loop ( with l= length of each section ) carries current i. Magnetic field at the centroid of the loop is
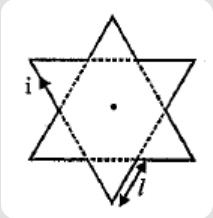
View SolutionAn equilateral triangular loop of wire of side / carries a current I. The magnetic field produced at the circumcentre of the loop is
View SolutionA rectangular loop of conductor of length a and breadtlı b carrying current / is shown in the figure. The magnetic field at the centre o of the loop is
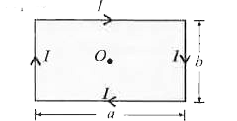
View Solution
