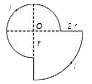
A current I flowing through the loop as shown in figure. The magnetic field at centre O is

A
7μ0I16R⊗
B
7μ0I16Rop∮
C
5μ0I16R⊗
D
5μ0I16Rop∮
Video Solution
Text Solution
The correct Answer is:A
B=BEP+BRS (into the paper )
=μ04π×3πI2R+μ04π×π2×I2R=716μ0IR
|
Similar Questions
Knowledge Check
A current I flows through a closed loop as shown in figure .The magnetic field at the centre O is
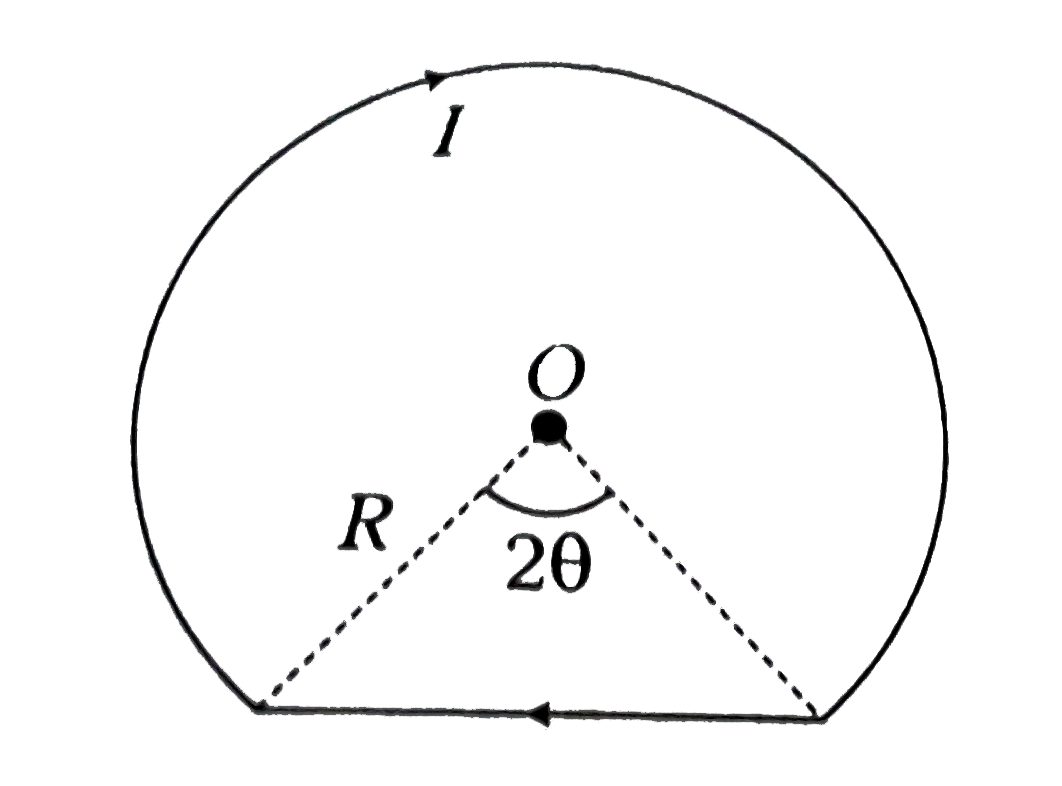 Aμ0I2πR(π−θ+tanθ)Bμ0I2πR(π−θ+sinθ)Cμ0I2πR(θ+sinθ)DNone of these
Aμ0I2πR(π−θ+tanθ)Bμ0I2πR(π−θ+sinθ)Cμ0I2πR(θ+sinθ)DNone of theseA current I flows through a closed loop as shown in figure. The magnetic field induction at the centre 0 is
 Aμ0I4πRθBμ0I4πR(θ+sinθ)Cμ0I4πR(π−θ+sinθ)Dμ0I4πR(π−θ+tanθ)
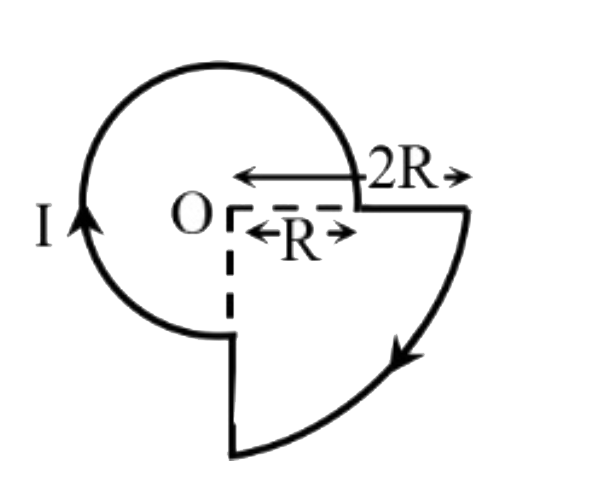
Aμ0I4πRθBμ0I4πR(θ+sinθ)Cμ0I4πR(π−θ+sinθ)Dμ0I4πR(π−θ+tanθ)A current /is flowing through the loop. The direction of the current and the shape of the loop are as shown in the figure. The magnetic field at the centre of the loop is μ0IR×(MA=R,MB=2R,∠DMA=90∘
 A516 ,but of the plane of the paper.B516, but into the plane of the paper.C716,but out of the plane of the paper.D716,but into the plane of the paper.
A516 ,but of the plane of the paper.B516, but into the plane of the paper.C716,but out of the plane of the paper.D716,but into the plane of the paper.
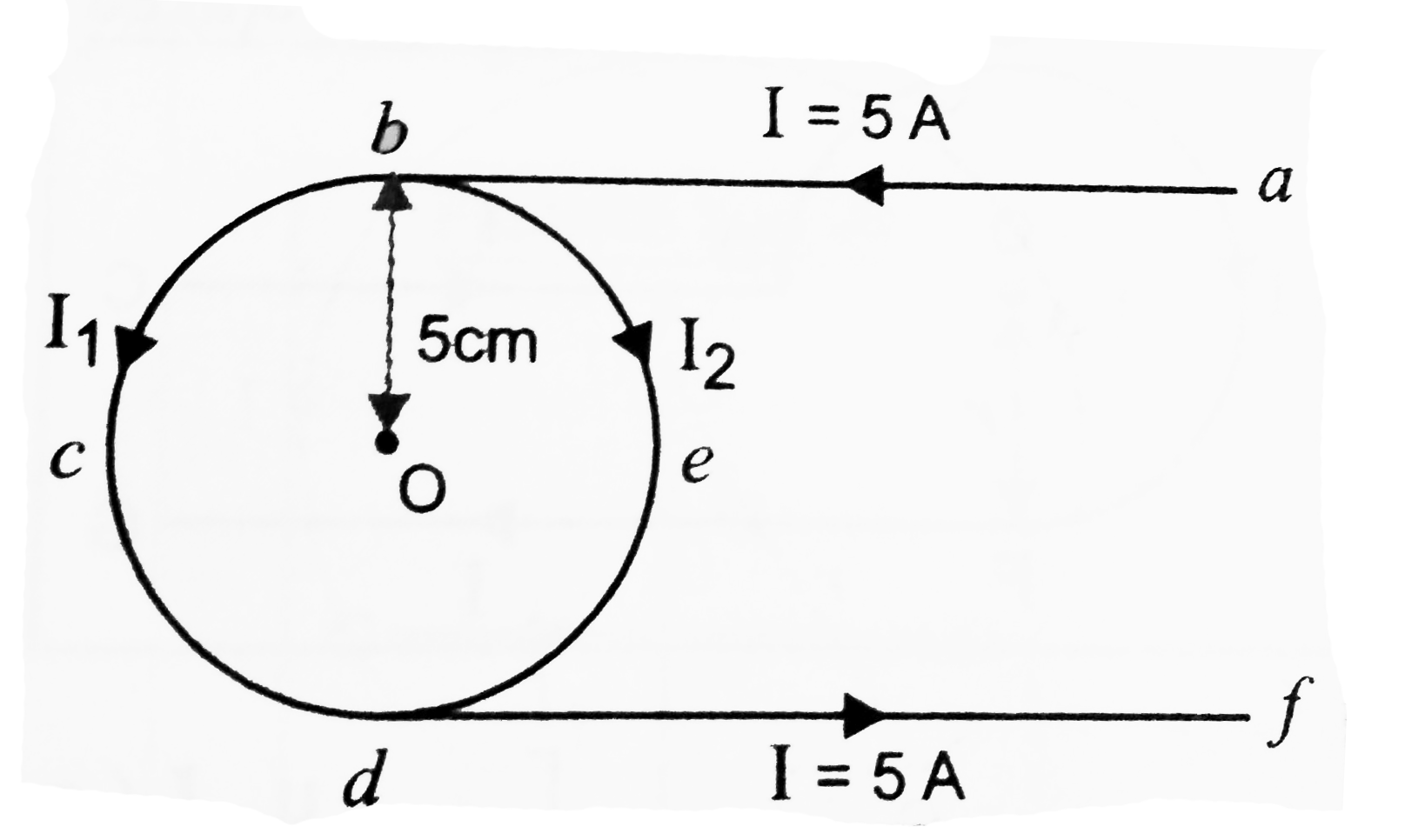
In the net work shown in figure,find the magnetic field at the centre O of the coil.
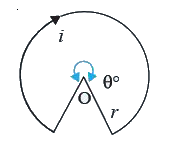
View SolutionA current i ampere flows in the loop having circular arc of radius r metre subtending an angle θ∘as shown in figure. The magnetic field at centre O of circle is
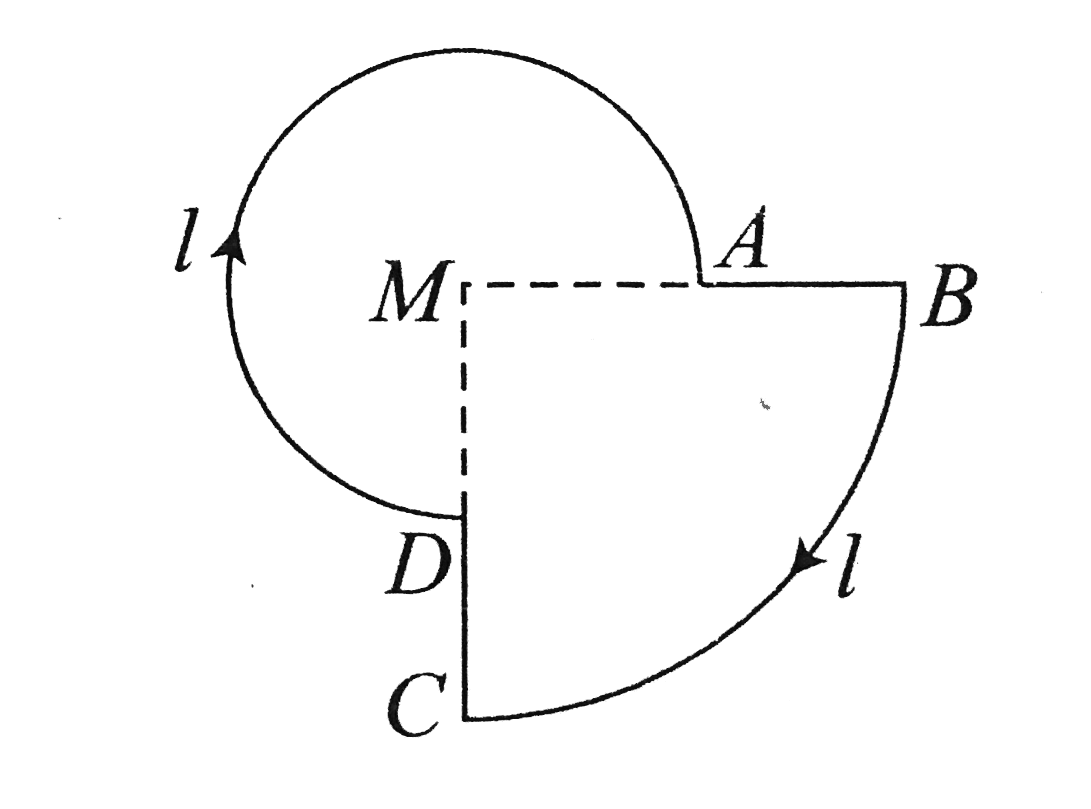
View SolutionA current I is flowing thorugh the loop. The direction of the current and the shape of the loop are as the shown in the figure. The magnetic fild at the centre of the loop is μ0IR times
(MA=R,MB=2R,∠DMA=90∘)
View SolutionA long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is

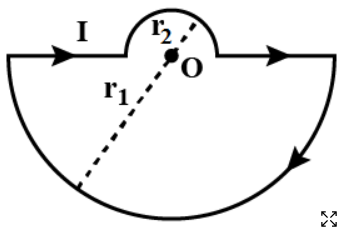
View SolutionIn the given loop the magnetic field at the centre O is
View Solution