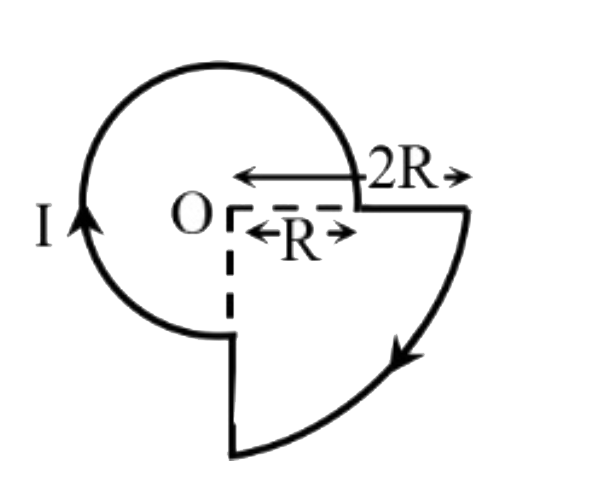
A current I is flowing thorugh the loop. The direction of the current and the shape of the loop are as the shown in the figure. The magnetic fild at the centre of the loop is μ0IR times
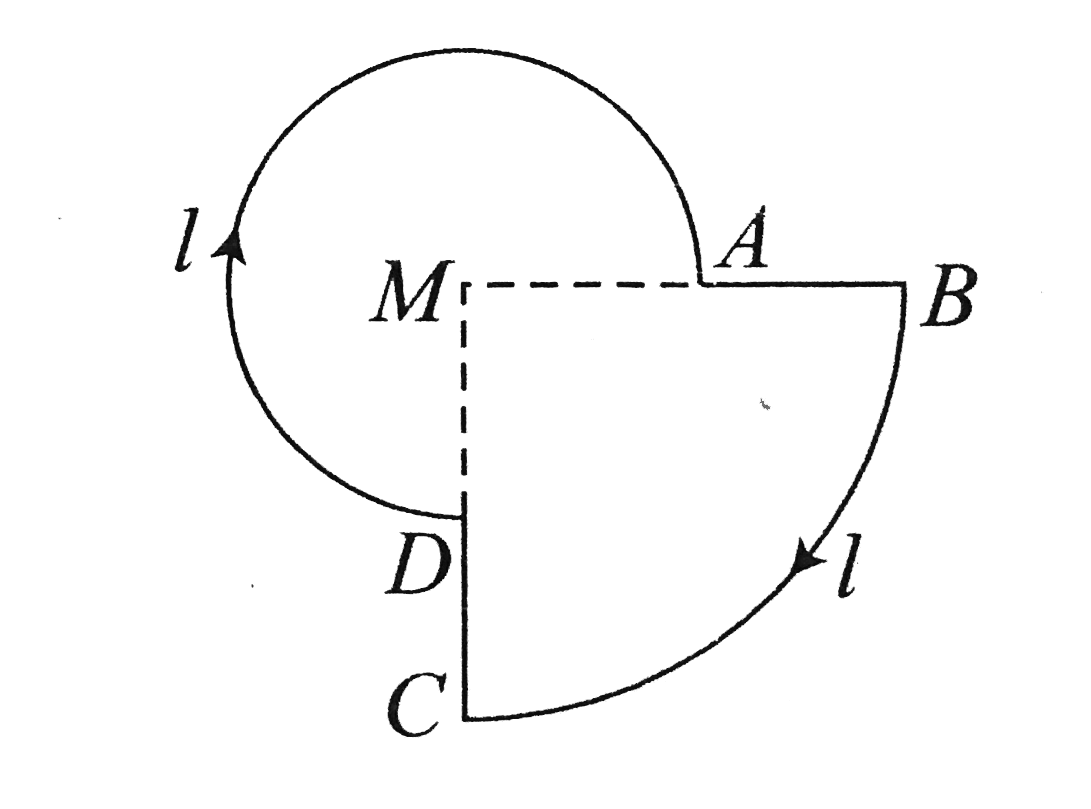
(MA=R,MB=2R,∠DMA=90∘)
516, but out of the plane of the paper.
716, but into of the plane of the paper.
516, but into of the plane of the paper.
716, but out of the plane of the paper.
The correct Answer is:B
Magnetic field at the centre M due to current through the curved portion DA is
→Bi=μ0I4πR×(3π2)=3μ0I8R⊗
[into the plane of paper]
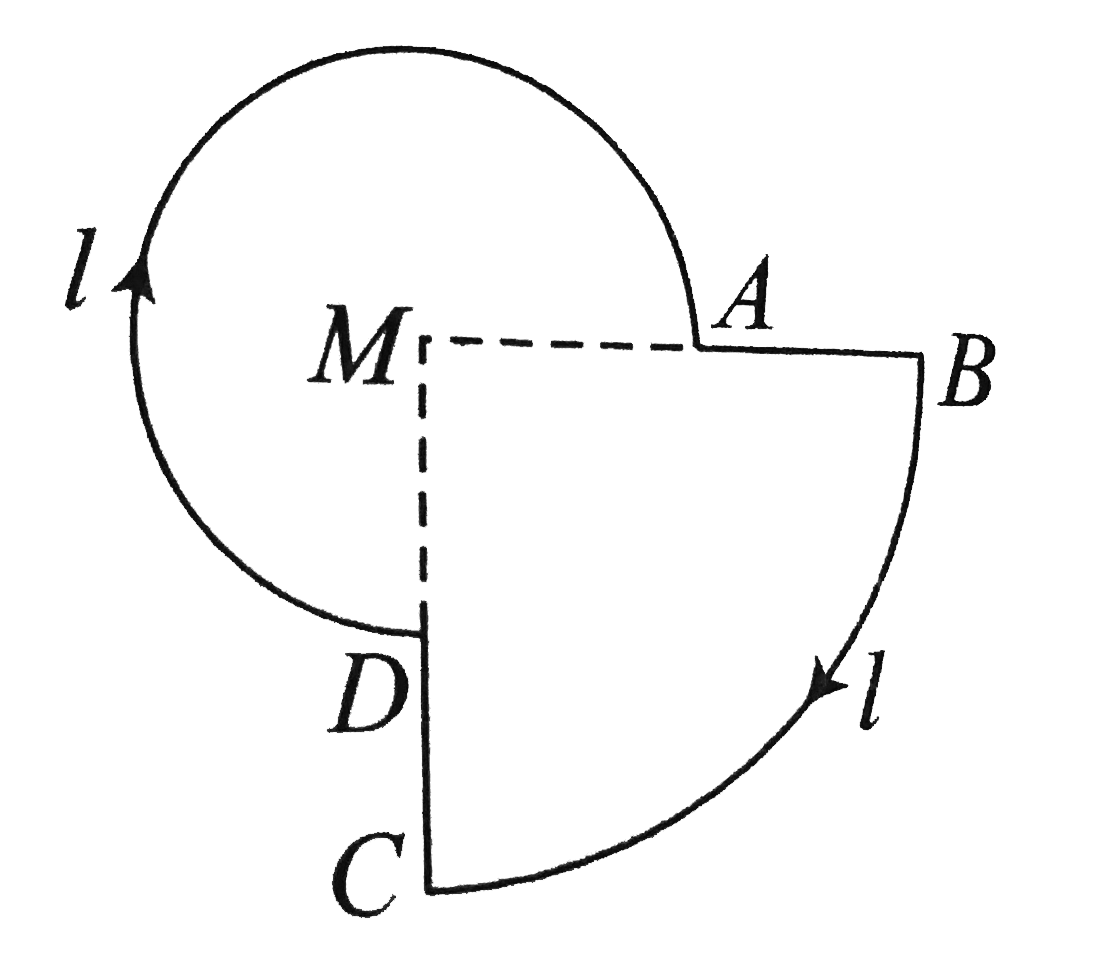
Magnetic field at the centre M due to current though the staight portion AB and CD will be zero.
Magnetic field at the centre M due to current through the curved portion BCis
→Bi=μ0I4π2R×π2=μ0I16R⊗ [into the plane of paper]
The resultant magnetic field at the point M is
→B=→B1+→B2=(3μ0I8R+μ0I16R)⊗=7μ0I16R⊗
[into the plane of paper]
Topper's Solved these Questions
- SOURCE AND EFFECT OF MAGNETIC FIELDBook:A2ZChapter:SOURCE AND EFFECT OF MAGNETIC FIELDExercise:Assertion- Reason
Explore 6 Videos
- SOURCE AND EFFECT OF MAGNETIC FIELDBook:A2ZChapter:SOURCE AND EFFECT OF MAGNETIC FIELDExercise:Section D - Chapter End Test
Explore 30 Videos
- SOURCE AND EFFECT OF MAGNETIC FIELDBook:A2ZChapter:SOURCE AND EFFECT OF MAGNETIC FIELDExercise:AIPMTNEET Questions
Explore 47 Videos
- SEMICONDUCTOR ELECTRONICSBook:A2ZChapter:SEMICONDUCTOR ELECTRONICSExercise:EXERCISE
Explore 29 Videos
- WAVE OPTICSBook:A2ZChapter:WAVE OPTICSExercise:Section D - Chapter End Test
Explore 29 Videos
Similar Questions
Knowledge Check
A current /is flowing through the loop. The direction of the current and the shape of the loop are as shown in the figure. The magnetic field at the centre of the loop is μ0IR×(MA=R,MB=2R,∠DMA=90∘
 A516 ,but of the plane of the paper.B516, but into the plane of the paper.C716,but out of the plane of the paper.D716,but into the plane of the paper.
A516 ,but of the plane of the paper.B516, but into the plane of the paper.C716,but out of the plane of the paper.D716,but into the plane of the paper.A square loop of side a carries a current I. The magnetic field at the center of the loop is
A2μ0I√2πaBμ0I√2πaC4μ0I√2πaDμ0IπaA current I flows through a closed loop as shown in figure. The magnetic field induction at the centre 0 is
 Aμ0I4πRθBμ0I4πR(θ+sinθ)Cμ0I4πR(π−θ+sinθ)Dμ0I4πR(π−θ+tanθ)
Aμ0I4πRθBμ0I4πR(θ+sinθ)Cμ0I4πR(π−θ+sinθ)Dμ0I4πR(π−θ+tanθ)
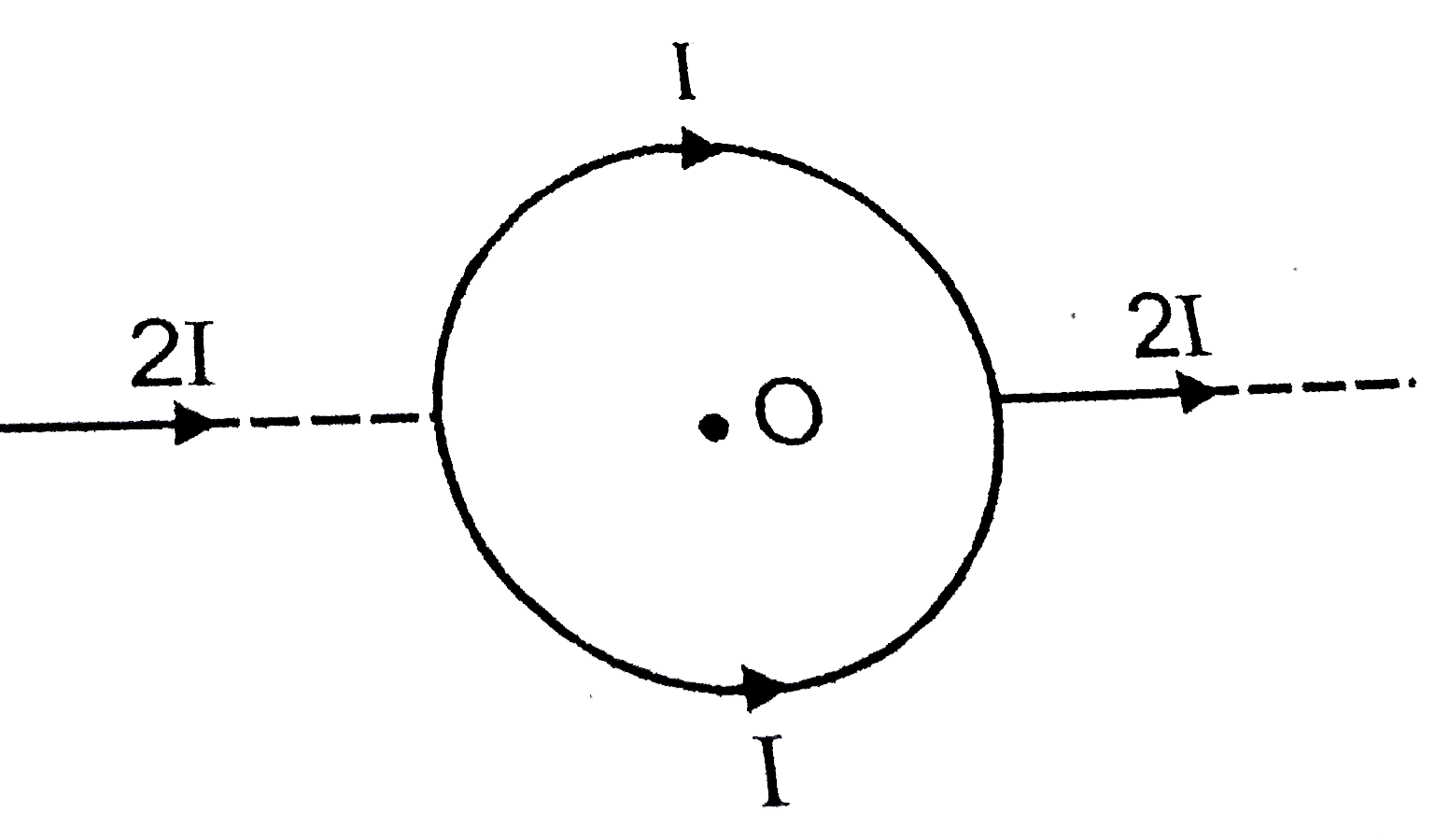
An infinite straigh conductor carrying current 2 I is split into a loop of radius r as shown in fig. the magnetic field at the centre of the coil is
View SolutionA rectangular loop of conductor of length a and breadtlı b carrying current / is shown in the figure. The magnetic field at the centre o of the loop is
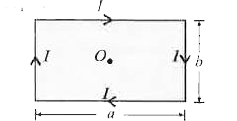
View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is

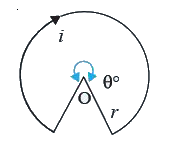
View SolutionA current i ampere flows in the loop having circular arc of radius r metre subtending an angle θ∘as shown in figure. The magnetic field at centre O of circle is
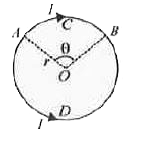
View SolutionEqual current I flows in two segments of a circular loop in the direction shown in figure. Radius of the loop is 7. The magnitude of magnetic field induction at the centre of the loop O is
View Solution