A current i ampere flows in a circular arc of wire whose radius is R, which subtend an angle 3π/2 radian at its centre. The magnetic induction B at the centre is

μ0iR
μ0i2R
2μ0iR
3μ0i8R
The correct Answer is:D
B=μ04π(2π−θ)iR=μ04π(2π−π2)×iR=3μ0i8R
Aliter : Magnetic field due to sector of coil-
B=μ04π⋅IθR
Here , θ=3θ2,B=μ0I4πR⋅3π2=3μ0I8R
Similar Questions
A circular arc of wire of radius of curvature r subtends an angle of p/4 radian at its centre. If i current is flowing in it then the magnetic induction at its centre is -
View SolutionConsider a circular arc of radius R which subtends an angle ϕ at its centre .Let us calculate the electric field strength at C
View Solution
Knowledge Check
An arc of a circle of radius R subtends an angle π2 at the centre. It carriers a current i. The magnetic field at the centre will be
Aμ0i2RBμ0i8RCμ0i4RD2μ0i5RAn are of a circle of a radius R subtends an angle π2 at the centre .it carries a current l. The magnetic field at the centre will be
Aμ0I2RBμ0I8RCμ0I4RDμ0I5RA current i ampere flows in the loop having circular arc of radius r metre subtending an angle θ∘as shown in figure. The magnetic field at centre O of circle is
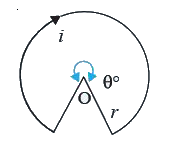 Aμ0Iθ4πrBμ0Iθ4πr2sinθCμ04irθ∘180∘Dμ(0)Isinθ4r
Aμ0Iθ4πrBμ0Iθ4πr2sinθCμ04irθ∘180∘Dμ(0)Isinθ4r
A piece of wire carrying a current of 6.00 A is bent in the form of a circular arc of radius 10.0 cm, and it subtends an angle of 120∘ at the centre. Find the magnetic field B due to this piece of wire at the centre.
View SolutionCurrent I A flowing in a circular coil of radius r. then the magnetic induction at the centre is B. If the current is doubled then the magnetic induction will be
View SolutionA current I ampere flows in the loop having circular arc of radius r metre subtending an angle 6 as shown in figure. The magnetic field, at center of circle is
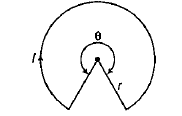
View SolutionTwo long straight wires are connected by a circular section which has a radius R. All the three segments lie in the same plane and carry a current I. The magnetic induction at the centre O of the circular segments is

View SolutionA battery is connected between two points AandB on the circumference of a uniform conducting ring of radius r and resistance R . One of the arcs AB of the ring subtends an angle θ at the centre . The value of the magnetic induction at the centre due to the current in the ring is
View Solution
