A composite metal bar of uniform section is made up of length 25 cm of copper, 10 cm of nickel and 15 cm of aluminium. Each part being in perfect thermal contact with the adjoining part. The copper end of the composite rod is maintained at and the aluminium end at . The whole rod is covered with belt so that there is no heat loss occurs at the sides. If , then what will be the temperatures of and junctions respectively
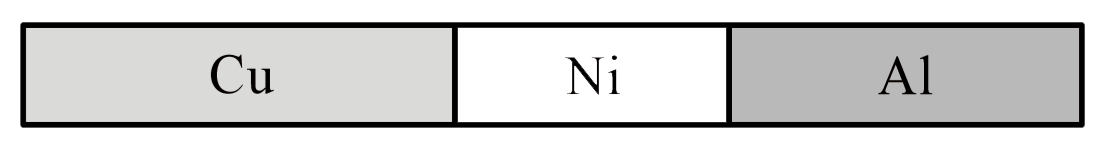
and
and
and
and C
The correct Answer is:B
All metal bars are connected in series
Now,
Hence if
if
Similar Questions
The ends of a metre stick are maintain at 100∘C and 0∘C . One end of a rod is mainntained 25∘C . Where should its other end be touched on the metre stick so that there is no heat current in the rod in steady state?
View SolutionOne face of a copper cube of edge 10 cm is maintained at 100∘C and the opposite face is maintained at 0∘C. All other surfaces are covered with an insulating material. Find the amount of heat flowing per second through the cube. Thermal conductivety of copper is 385Wm−1^(@)C^(-1).
View Solution
Knowledge Check
The end A of rod AB of length 1 m is maintained at 80∘C and the end B at 0∘C. The temperature at a distance of 60 cm from the end A is
A16∘CB32∘CC48∘CD64∘CThe ends of a metre stick are maintained at 100∘C and 0∘C. One end of a rod is maintained at 25∘C. Where should its other end be touched on the metre stick so that there is no heat current in the rod in steady state?
A25cm form the hot endB40cm from the cold endC25cm from the cold endD60cm from the cold endA large cylindrical rod of length L is made by joining two identical rods of copper and steel of length (L2) each. The rods are completely insulated from the surroundings. If the free end of copper rod is maintained at 100∘C and that of steel at 0∘C then the temperature of junction is (Thermal conductivity of copper is 9 times that of steel)
A90∘CB50∘CC10∘CD67∘C
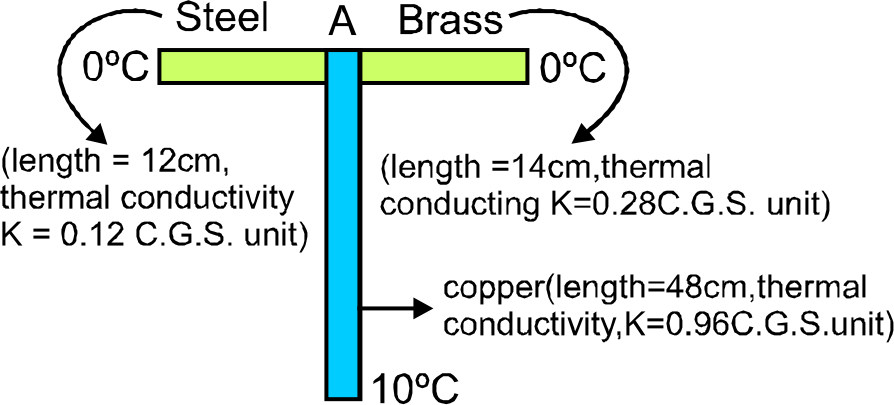
Three rods of copper, brass and steel are joined together to form T shape as shown in figure. The cross sectional area of each rod is 4cm2 the end of copper rod is maintained at 10∘C and the ends of brass and steel rods at 0∘C assume there is no loss of heat to surrounding. What is temperature of junction point A in .∘C
View SolutionOn heating one end of a rod the temperature of the whole rod will be uniform when .
View SolutionA composite rod of uniform cross-section has copper and aluminium sections of the same length in good thermal contact. The ends of the rod, which is well-lagged, are maintained at 100∘C and at0∘C as shown in the diagram (Figure-4.33). The thermal conductivityof copper is twice that of aluminium.
Which one of the following graphs represents the variation of temperature T with x along the rod in the steady state ?

View SolutionA composite rod consists of a steel rod of length 25cm and area 2A and a copper rod of length 50cm and area A. The composite rod is subjected to an axial load F. If the Young's moduli of steel and copper are in the ratio 2:1 then
View SolutionA uniform rod of length 15 cm is suspended from a fixed point by two strings of length 9 cm and 12 cm attached at its ends. If the inclination of the rod to the vertical is θ then sinθ is equal to
View Solution