Two rods (one semi-circular and other straight) of same material and of same cross-sectional area are joined as shown in the figure. The point A and B are maintained at different temperature. Find the ratio of the heat transferred through a cross-section of a semi-circular rod to the heat transferred through a cross section of the straight rod in a given time.

2:π
1:2
π:2
3:2
The correct Answer is:A
Since , dQdt=KA△Tl
⇒dQdt∝1l⇒(dQdt)semicircular(dQdt)straight=lstraightlsemicircular=2rπr=2π
Similar Questions
(a) Three rod of lengths 20cm each and area of cross-section 1cm2 are joined to form a triangle ABC. The conductivities of the rods are KAB=50J/m−s−.∘C,KBC=200J/m−s−.∘C and KAC=400J/m−s−.∘C. The junctions A,B and C are maintained at 40∘C, 80∘C and 80∘C respectively. Find the rate of heat flowing through the rods AB,AC and BC.
(b) A semicircular rod is joineted as its end to a straight rod of the same material and the same cross-sectional area. The straight rod forms a diameter of the other rod. The junctions are maintained at different temperatures. Find the ratio of the heat transferred through a cross-section of the simicircular rod to the heat transferred through a cross-section of the straight rod in a given time.
View SolutionA semicircular rods is joined at its end to a straight rod of the same material and the same cross-sectional area. The straight rod formss a diameter of the other rod. The junction are maintaine dat different temperature. Find the ratio of the heat transffered through a cross section of the straigh rod in a given time.
View Solution
Knowledge Check
Two rods one is semi circular of thermal conductivity K1 and otheir is straight of thermal conductivity K2 and of same cross sectional area are joined as shown in the The points A and B are maintained at same temperature difference. If rate of flow of heat is same in two rods then K1/K2 is
 .A2:πB1:2Cπ:2D3:2
.A2:πB1:2Cπ:2D3:2A metal rod of length 2 m has cross sectional areas 2 A and A as shown in figure. The ends are maintained at temperatures 100° C and 70° C . The temperature at middle point C is
 A80∘CB85∘CC90∘CD95∘C
A80∘CB85∘CC90∘CD95∘CA uniform cylindrical rod of length L and cross-sectional area by forces as shown in figure.

The elongation produced in the rod isA3FL8AYB3FL5AYC8FL3AYD5FL3AY
Three rods of same material and of equal cross sectional area and length have been connected together as shown in the figure. The temperature of the junction of the rods approximately is
View SolutionThree rods are made from the same material and having the same cross-sectional area and length have been joined as shown in the figure.
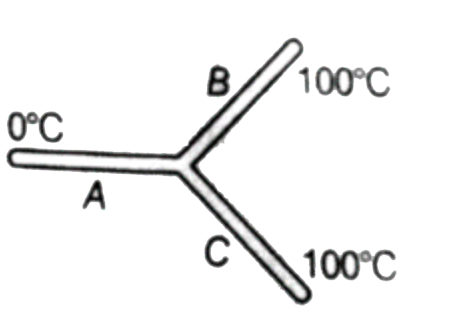
The left end and right end are kept 0∘Cand100∘C , respectively . The temperature of the junction of three rods will be
View SolutionTwo rods of different materials having differnet lengths and same cross sectional areas are joined end to end in a straight line. The free ends of this compound rod are maintained at different temperatures The temperature gradient in each rod will be .
View SolutionThree rods A,B and C of the same length and cross- sectional area are joined in series as shown. The temperature at the junction of A and B, in equilibriu, is
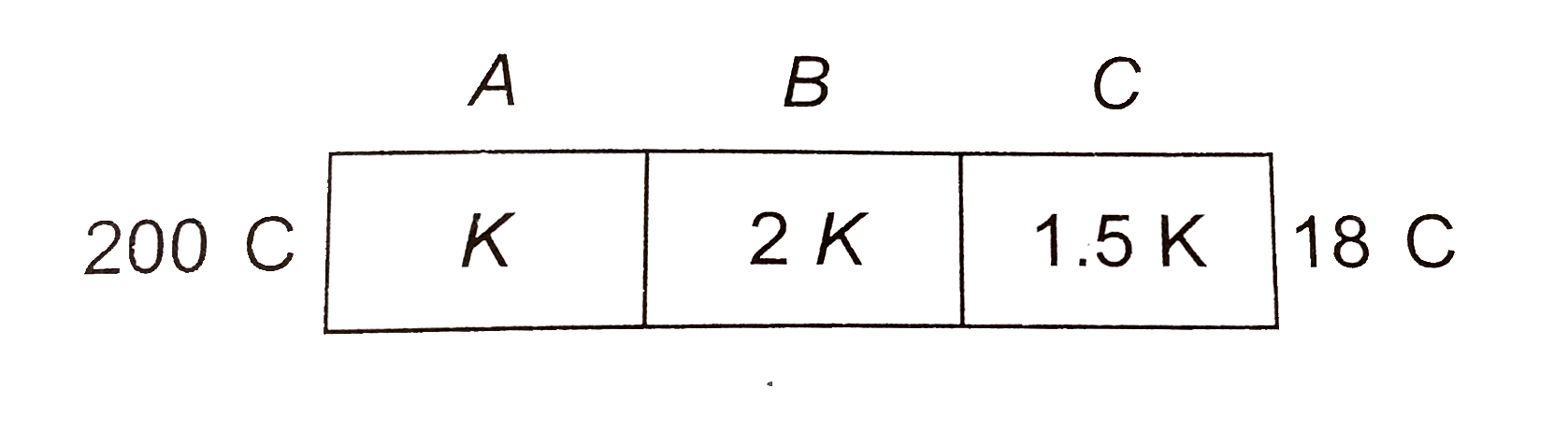
View SolutionThree conducting rods of same material and cross-section are shown in figure. Temperatures of A,D and C are maintained at 20∘C,90∘Cand0∘C. The ratio of lengths BD and BC if there is no heat flow in AB is

View Solution