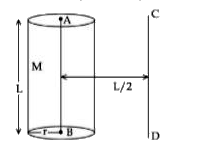
The solid cylinder of length 80 cm and mass M has a radius of 20 cm. Calculate the density of the material used if the moment of inertia of the cylinder about an axis CD parallel to AB as shown in figure is 2.7 kg $m^{2}$ .

A

$1.49 \times 10^{2} k g / m^{3}$

B

$7.5 \times 10^{1} k g / m^{3}$

C

$14.9 k g / m^{3}$

D

$7.5 \times 10^{2} k g / m^{3}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Parallel axis theorem
$I = I_{C M} + M d^{2}$
$I = \frac{M r^{2}}{2} + M {(\frac{L}{2})}^{2}$
$2.7 = M \frac{{(0.2)}^{2}}{2} + M {(\frac{0.8}{2})}^{2}$
$2.7 = M [\frac{2}{100} + \frac{16}{100}]$
M=15 kg
implies $ρ = \frac{M}{π r^{2} L} = \frac{15}{π {(0.2)}^{2} \times 0.8}$
= $1.492 \times 10^{2} k g / m^{3}$

Updated on:21/07/2023

|

Class 11 PHYSICS RIGID BODY DYNAMICS

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile