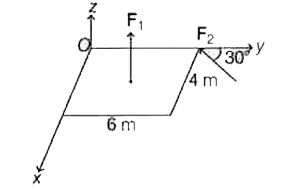
A slab is subjected to two forces vec F(1) and vec F(2) of same magnit

When force $- \to F_{1}, - \to F_{2}, - \to F_{3} \dots... - \to F_{n}$ act on a particle , the particle remains in equilibrium . If $- \to F_{1}$ is now removed then acceleration of the particle is

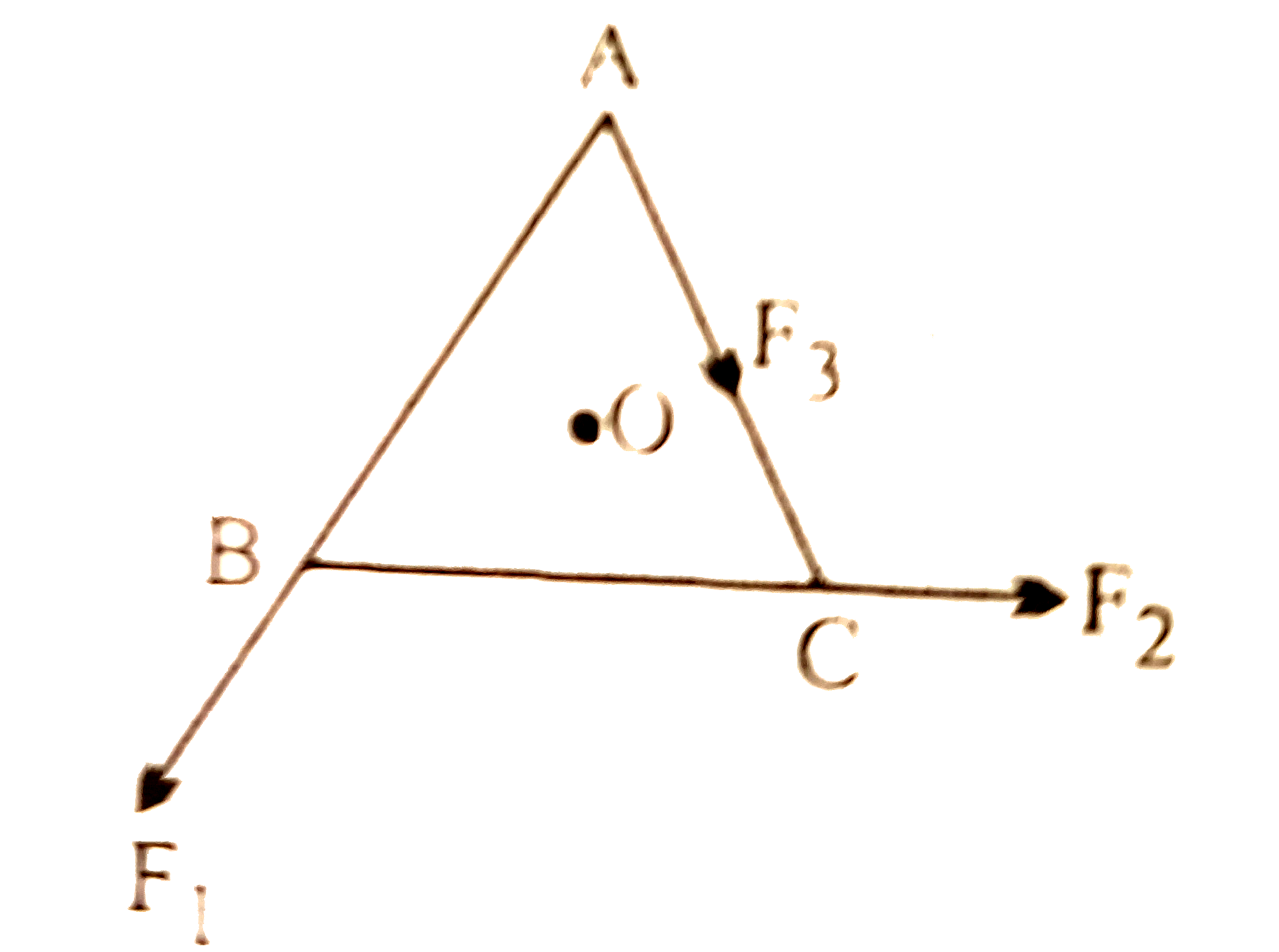
View Solution

ABC एक समबाहु त्रिभुज है जिसका केंद्र O है, $- \to F_{1}, - \to F_{2}$ तथा $- \to F_{3}$ क्रमश AB, BC तथा AC दिशा में लगे बल हैं । यदि O के परितः कुल बल आघूर्ण शून्य हो, तो $- \to F_{3}$ का मान होगा-
ocr_image

View Solution

दिखाएं गए चित्रानुसार एक तख्त पर समान परिमाण F के दो बल $F_{1}$ तथा $F_{2}$ लगाए गए है। बल $F_{2}$ XY-समतल में है, जबकि बल, $F_{1}$ , z-दिशा के अनुदिश बिंदु $(2 ˆ i + 3 ˆ j)$ पर लगा है। बिंदु O के सापेक्ष इन बलों का आघूर्ण होगा
ocr_image

View Solution

दिखाये गये चित्रानुसार एक तख्त पर समान परिमाण F के दो बल ${\to F}_{1}$ तथा ${\to F}_{2}$ लगाये गये है। बल ${\to F}_{2} X Y$ समतल में है जबकि बल $F_{1} Z -$ दिशा के अनुदिश बिन्दु $(\to 2 i + \to 3 j)$ पर लगा है। बिन्दु 0 के सापेक्ष इन बलों का आघूर्ण होगा
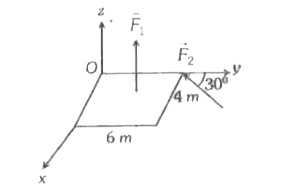
ocr_image

View Solution

A slab is subjected to two forces vec F_(1) and vec F_(2) of same magnitude F as shown in the figure . Force vec F_(2) is in XY-plane while force F_(1) acts along z-axis at the point (2 vec I + 3 vec j) .The moment of these forces about point O will be :

View Solution

A body is moving under the action of two force vec(F_(1)=2hati-5hatj , vec(F_(2)=3hati-4hatj . Its velocity will become uniform under a third force vec(F_(3) given by.

View Solution

A body is moving under the action of two force $- --------- \to F_{1} = 2 ˆ i - 5 ˆ j$ , $- --------- \to F_{2} = 3 ˆ i - 4 ˆ j$ . Its velocity will become uniform under a third force $- \to F_{3}$ given by.

View Solution

ABC is an equilateral triangle with O as its centre vec(F_(1)),vec(F_(2)) " and " vec(F_(3)) represent three forces acting along the sides AB, BC and AC respectively. If the torque about O is zero then the magnitude of vec(F_(3)) is

View Solution

A slab is subjected to two forces ${\to F}_{1} and {\to F}_{2}$ of same magnitude F as shown in the figure . Force ${\to F}_{2}$ is in XY-plane while force $F_{1}$ acts along z-axis at the point $(2 \to I + 3 \to j)$ .The moment of these forces about point O will be :

The correct Answer is:D

$τ_{0} = {\to r}_{1} \times {\to F}_{1} + {\to r}_{2} \times {\to F}_{2}$
$= (2 ˆ i + 3 ˆ j) \times F (ˆ k) + 6 ˆ j \times (\frac{F}{2} (- ˆ i) + \frac{F \sqrt{3}}{2} (- ˆ j))$
$= 2 F (- ˆ j) + 3 F (ˆ i) + 3 F (ˆ k) + 0$
$= (3 ˆ i - 2 ˆ j + 3 ˆ k) F$

Similar Questions

Recommended Questions

A slab is subjected to two forces →F1and→F2 of same magnitude F as shown in the figure . Force →F2 is in XY-plane while force F1 acts along z-axis at the point (2→I+3→j) .The moment of these forces about point O will be :

The correct Answer is:D

τ0=→r1×→F1+→r2×→F2 =(2ˆi+3ˆj)×F(ˆk)+6ˆj×(F2(−ˆi)+F√32(−ˆj)) =2F(−ˆj)+3F(ˆi)+3F(ˆk)+0 =(3ˆi−2ˆj+3ˆk)F

Similar Questions

Recommended Questions

A slab is subjected to two forces ${\to F}_{1} and {\to F}_{2}$ of same magnitude F as shown in the figure . Force ${\to F}_{2}$ is in XY-plane while force $F_{1}$ acts along z-axis at the point $(2 \to I + 3 \to j)$ .The moment of these forces about point O will be :

$τ_{0} = {\to r}_{1} \times {\to F}_{1} + {\to r}_{2} \times {\to F}_{2}$
$= (2 ˆ i + 3 ˆ j) \times F (ˆ k) + 6 ˆ j \times (\frac{F}{2} (- ˆ i) + \frac{F \sqrt{3}}{2} (- ˆ j))$
$= 2 F (- ˆ j) + 3 F (ˆ i) + 3 F (ˆ k) + 0$
$= (3 ˆ i - 2 ˆ j + 3 ˆ k) F$