A wheel of radius $0.4 m$ can rotate freely about its axis as shown in the figure. A string is wrapped over its rim and a mass of $4 k g$ is hung. An angular acceleration of $8 r a d / s^{2}$ is produced in it due to the torque. Then, the moment of inertia of the wheel is ( $g = 10 m / s^{2}$ )

$2 k g - m^{2}$

$1 k g - m^{2}$

$4 k g - m^{2}$

$8 k g - m^{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

$τ = F r_{⊥} = 4 \times 10 \times 0.4 = 16 N - m$
Now $τ = I α \Rightarrow I = \frac{16}{8} = 2 k g - m^{2}$

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Similar Questions

A wheel of radius 0.4 m can rotated freely about its axis as shown in the figure. A string is wrapped over its rim and a mass of 4 kg is hung, An angular acceleration of 8 rad $s^{- 2}$ is produced in it due to the torque. Then moment inergia of the wheel is (g = $10 m s^{- 2}$ )

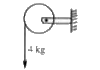
View Solution
A wheel of radius 20 cm can rotate about its centre. A string is wrapped over its rim and is pulled by a force of 10N tangential to pulley. If the angular acceleration produced is 4 rad $s^{- 2}$ then the moment of inertia of the wheel in kg $m^{2}$ is
View Solution
A constant torque of 3.14 N mis exerted on a pivoted wheel. If the angular acceleration of the wheel is $4 π rad/ s^{2}$ then the moment of inertia of the wheel is
View Solution
A wheel of radius $0.4$ m can rotated freely about its axis as shown in the figure. A string is wrapped over its rim and a mass of 4 kg is hung, An angular acceleration of $8 {rad - s}^{- 2}$ is produced in it due to the torque. Then moment inertia of the wheel is $(g = 10 {ms}^{- 2})$

View Solution
A wheel of radius 20 cm rotate about its centre. A string is wrapped over its rim and is pulled by a force of 10 N tangential to pulley. If the angular acceleration produced is ${4 rad s}^{- 2}$ , then the moment of inertia of the wheel in kg $m^{2}$ is
View Solution
A wheel of radius 20 cm and moment of inertia 1 kgm^2 can rotate about its centre.A string is wrapped over its rim and is pulled by a force 'F' tangential to the rim of wheel.If angular acceleration produced is 2 rad/ s^2 then the value of force 'F' is
View Solution
A wheel of radius 20 cm and moment of inertia $1$ kgm^2 can rotate about its centre.A string is wrapped over its rim and is pulled by a force 'F' tangential to the rim of wheel.If angular acceleration produced is $2$ rad/s^2 then the value of force 'F' is
View Solution
A wheel of radius 0.4m can rotate freely about its axis as shown in the figure. A string is wrapped over its rim and a mass of 4 kg is hung. An angular acceleration of 8 rad//s^(2) is produced in it due to the torque. Then, the moment of inertia of the wheel is ( g=10m//s^(2) )
View Solution

A wheel of radius 0.4m can rotate freely about its axis as shown in the figure. A string is wrapped over its rim and a mass of 4kg is hung. An angular acceleration of 8rad/s2 is produced in it due to the torque. Then, the moment of inertia of the wheel is (g=10m/s2)

The correct Answer is:A

τ=Fr⊥=4×10×0.4=16N−m Now τ=Iα⇒I=168=2kg−m2

Similar Questions

Recommended Questions

A wheel of radius $0.4 m$ can rotate freely about its axis as shown in the figure. A string is wrapped over its rim and a mass of $4 k g$ is hung. An angular acceleration of $8 r a d / s^{2}$ is produced in it due to the torque. Then, the moment of inertia of the wheel is ( $g = 10 m / s^{2}$ )

$τ = F r_{⊥} = 4 \times 10 \times 0.4 = 16 N - m$
Now $τ = I α \Rightarrow I = \frac{16}{8} = 2 k g - m^{2}$