F=(3,−4,2) & r=(2,2,1) then find torque about the origin.
8ˆi−ˆj−14ˆk
8ˆi+ˆj−14ˆk
8ˆi−ˆj+14ˆk
8ˆi+ˆj+14ˆk
To find the torque τ about the origin given the force vector F=(3,−4,2) and the position vector r=(2,2,1), we will use the formula for torque:
τ=r×F
1. Identify the vectors:
- The position vector r can be expressed as:
r=2^i+2^j+1^k
- The force vector F can be expressed as:
F=3^i−4^j+2^k
2. Set up the determinant for the cross product:
We will use the determinant to calculate the cross product:
τ=∣∣
∣
∣∣^i^j^k2213−42∣∣
∣
∣∣
3. Calculate the determinant:
- Expanding the determinant:
τ=^i∣∣∣21−42∣∣∣−^j∣∣∣2132∣∣∣+^k∣∣∣223−4∣∣∣
4. Calculate each of the 2x2 determinants:
- For ^i:
∣∣∣21−42∣∣∣=(2)(2)−(1)(−4)=4+4=8
- For −^j:
∣∣∣2132∣∣∣=(2)(2)−(1)(3)=4−3=1⇒−1^j
- For ^k:
∣∣∣223−4∣∣∣=(2)(−4)−(2)(3)=−8−6=−14
5. Combine the results:
Putting it all together:
τ=8^i−1^j−14^k
6. Final result:
Thus, the torque about the origin is:
τ=8^i−1^j−14^k
- The position vector r can be expressed as:
r=2^i+2^j+1^k
- The force vector F can be expressed as:
F=3^i−4^j+2^k
We will use the determinant to calculate the cross product:
τ=∣∣
∣
∣∣^i^j^k2213−42∣∣
∣
∣∣
- Expanding the determinant:
τ=^i∣∣∣21−42∣∣∣−^j∣∣∣2132∣∣∣+^k∣∣∣223−4∣∣∣
- For ^i:
∣∣∣21−42∣∣∣=(2)(2)−(1)(−4)=4+4=8
- For −^j:
∣∣∣2132∣∣∣=(2)(2)−(1)(3)=4−3=1⇒−1^j
- For ^k:
∣∣∣223−4∣∣∣=(2)(−4)−(2)(3)=−8−6=−14
Putting it all together:
τ=8^i−1^j−14^k
Thus, the torque about the origin is:
τ=8^i−1^j−14^k
Topper's Solved these Questions
Similar Questions
The body in figure shown is pivoted at O and two forces acts on it as shown
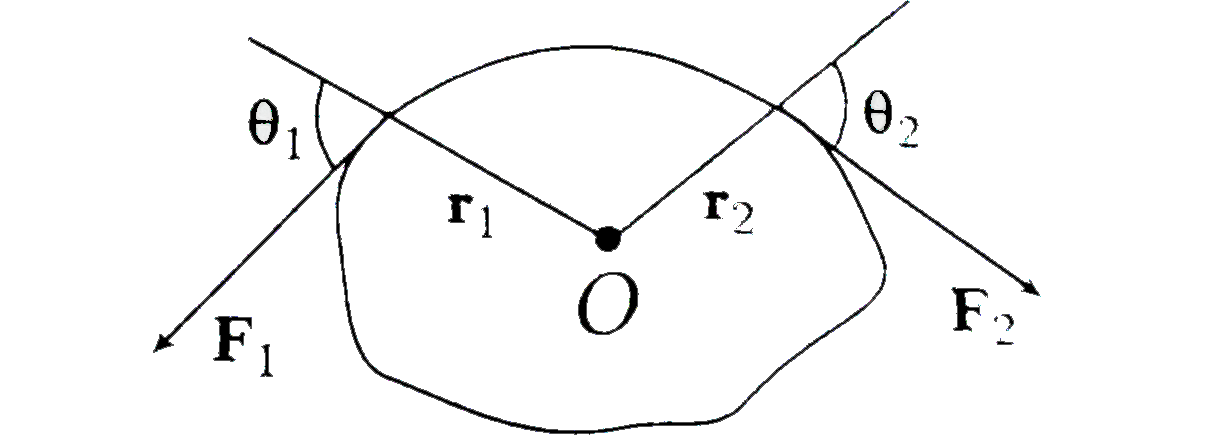
(i) Find an expression of the net torque on the body about the pivot
(ii) If r1=1.30m,r2=2.15m,F1=4.20N,F2=4.90N,θ1=75∘ and θ2=60∘, what is the net torque about the pivot ?
View SolutionA force F=(2ˆi+3ˆj−2ˆk)N is acting on a body at point (2m, 4m,−2m). Find torque of this force about origin.
View Solution
Knowledge Check
A force F=(2ˆi+3ˆj−ˆk)N is acting on a body at a position r=(6ˆi−3ˆj−2ˆk). Calculate the torque about the origin
A(3ˆi+2ˆj+12ˆk)NmB(9ˆi+2ˆj+7ˆk)NmC(ˆi+2ˆj+12ˆk)NmD(3ˆi+12ˆj+ˆk)NmIf →F is the force acting in a particle having position vector →r and →τ be the torque of this force about the origin, then
A→r.→T=0 and →F.→T=0Bvec(r ) .vec(T) cancel(=) but →F.→T=0Cvec(r ) .vec(T) cancel(=) but vec(F).vec(T)cancel(=)0Dvec( r ) . vec( T )cancel( =) 0 and vec(F) .vec(T)cancel(=)0A force F=2ˆi+3ˆj−ˆk acts at a point (2,-3,1). Then magnitude of torque about point (0,0,2) will be
A6 unitsB3√5 unitsC6√5 unitsDNone of these
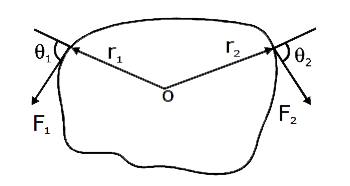
The body in shown figure is pivoted at O, and two forces act on its as shown.
If r1=1.30m,r2=2.15m,F1=4.20N,
F2=4.90N,θ1=45∘ and θ2=60∘, What is the net torque about the privot ? what is the net torque about the pivot?
View Solutionf(x) is a polynomial of degree 3 passing through the origin having local extrema at x=±2 Statement 1 : Ratio of areas in which f(x) cuts the circle x2+y2=36is1:1. Statement 2 : Both y=f(x) and the circle are symmetric about the origin.
View SolutionIf →F is the force acting in a particle having position vector →r and →τ be the torque of this force about the origin, then
View SolutionA faorce F=5ˆi+2ˆj−5ˆk acts on particles whose position vector is r=→j−2→j+→k. What is the torque about the origin ?
View SolutionA particle of mass 0.2 kg moves along a path given by the relation : →r=2cosωtˆi+3sinωtˆj. Then he torque on the particle about the origin is :
View Solution

