is non zero vector then
x
x
x
To solve the problem, we need to analyze the properties of a non-zero vector →A and evaluate the given options based on vector operations.
1. Understanding the Dot Product:
The dot product of a vector with itself is given by:
→A⋅→A=|→A|2
Since →A is a non-zero vector, its magnitude |→A| is not zero. Therefore, →A⋅→A≠0.
Conclusion: Option 1 (→A⋅→A=0) is incorrect.
Hint: Remember that the dot product of a vector with itself gives the square of its magnitude.
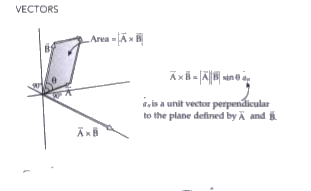
2. Understanding the Cross Product:
The cross product of a vector with itself is given by:
→A×→A=0
This is because the sine of the angle between the same vectors is zero (the angle is 0 degrees), leading to:
|→A|⋅|→A|⋅sin(0)=0
Conclusion: Option 2 (→A×→A=0) is correct.
Hint: The cross product of any vector with itself is always zero.
3. Evaluating Other Options:
- Option 3 (→A×→A<0): This is incorrect because the cross product is zero, not less than zero.
- Option 4 (→A×→A>0): This is also incorrect for the same reason; the cross product is zero, not greater than zero.
Conclusion: Options 3 and 4 are incorrect.
Final Answer:
The only correct option is Option 2: →A×→A=0.
The dot product of a vector with itself is given by:
→A⋅→A=|→A|2
Since →A is a non-zero vector, its magnitude |→A| is not zero. Therefore, →A⋅→A≠0.
The cross product of a vector with itself is given by:
→A×→A=0
This is because the sine of the angle between the same vectors is zero (the angle is 0 degrees), leading to:
|→A|⋅|→A|⋅sin(0)=0
- Option 3 (→A×→A<0): This is incorrect because the cross product is zero, not less than zero.
- Option 4 (→A×→A>0): This is also incorrect for the same reason; the cross product is zero, not greater than zero.
The only correct option is Option 2: →A×→A=0.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The cross product of two vectors gives a vector perpendicular to the plane containing the vectors.
If →a and →b are non-zero vectors, then →a⋅(→a×→b)= _________A0B→0C→aD→bIf →a is a non-zero vector of modulus a and λ is a non-zero scalar and λ→a is a unit vector, then
Aλ=±1B→a=|λ|C→a=1|λ|D→a=1λIf ¯a is a non-zero vector of modulus a and m is non-zero scalar, then m¯a is a unit vector, if
Am=±1Bm=|¯a|Cm=1|¯a|Dm=±2
If →a is a non zero vecrtor iof modulus a and m is a non zero scalar such that ma is a unit vector, write the value of m.
View SolutionIf →d=→a×→b+→b×→c+→c×→a is non-zero vector and ∣∣(→d⋅→c)(→a×→b)+(→d⋅→a)(→b×→c)+(→d⋅→b)(→c×→a)∣∣=0, then a.|→a|=∣∣→b∣∣=|→c| b. |→a|+∣∣→b∣∣+|→c|=|d| c. →a,→b,and→c are coplanar d. none of these
View SolutionIf →a is perpendicular to →b and →r is non-zero vector such that p→r+(→r.→a)→b=→c, then →r= →cp−(→a.→c)→bp2 (b) →ap−(→⋅→b)→ap2 →ap−(→a.→b)→cp2 (d) →cp2−(→a.→c)→bp
View SolutionIf →x and →y be two non - zero vectors such that |→x+→y|=|→x| and 2→x+λ→y is perpendicular to →y then the value of λ is _______ .
View Solution→a,→b,→c are three non zero vectors no two of which are collonear and the vectors →a+→b be collinear with →c,→b+→c to collinear with →a then →a+→b+→c the equal to ? (A) →a (B) →b (C) →c (D) None of these
View Solution

