Figure shows three resistor configurations $R_{1}, R_{2}$ and $R_{3}$ connected to $3 V$ battery. If the power dissipated by the configurations $R_{1}, R_{2}$ and $R_{3}$ is $P_{1}, P_{2}$ and $P_{3}$ respectively, then

A

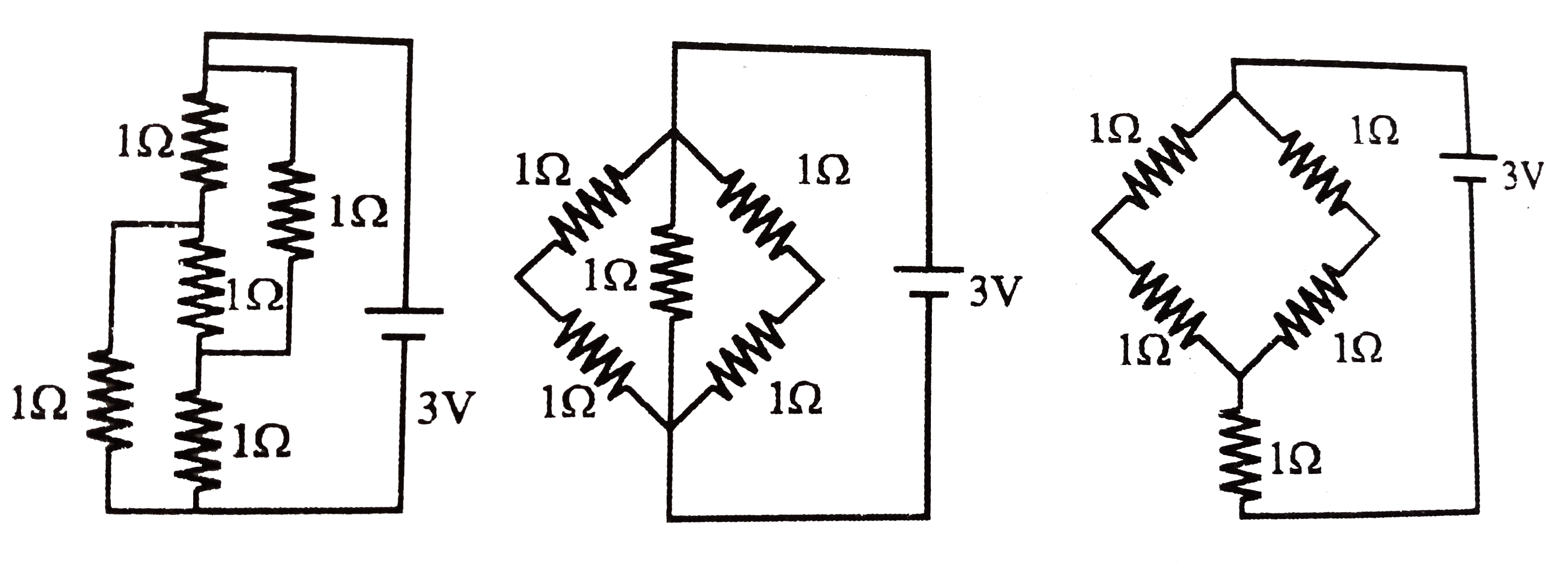
$P_{1} > P_{2} > P_{3}$

B

$P_{1} > P_{3} > P_{2}$

C

$P_{2} > P_{1} > P_{3}$

D

$P_{3} > P_{2} > P_{1}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

(i) Wheatstone bridge balance
$R_{1} = 1 Ω$
(ii) $\frac{1}{R_{2}} = \frac{1}{2} + 1 + \frac{1}{2} = \frac{1 + 2 + 1}{2} \Rightarrow R_{2} = \frac{1}{2} Ω$
(iii) $R_{3} = 1 + 1 = 2 Ω$
Since, $P = \frac{V^{2}}{R} \Rightarrow P \propto \frac{1}{R}$
$R_{3} > R_{1} > R_{2}$
hence, $P_{2} > P_{1} > P_{3}$

Updated on:21/07/2023

|

Class 12 PHYSICS CURRENT ELECTRICITY

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile