If qf is the free charge on the capacitor plates and qb is the bound charge on the dielectric slab of dielectric constant k placed between the capacitor plates, then bound charge qb can be expressed as :
qb=qf(1−1k)
qb=qf(1+1k)
qb=qf(1−1√k)
qb=qf(1+1√k)
The correct Answer is:A
σb=σf(1−1k)
qb=qf(1−1k).
Similar Questions
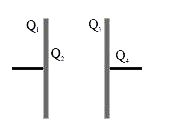
दो एकसमान धातु प्लेटों पर क्रमशः धन आवेश Q1,Q2,Q3 तथा Q4 दिये गये हैं । अब यदि इन प्लेटों को पास लाकर C धारिता का समान्तर पट्टिका संधारित्र बनाया जाता है, तब प्लेटों के बीच विभवान्तर होगा
View SolutionA dielectric slab is inserted between the plates of a capacitor. The charge on the capacitor is Q and the magnitude of the induced charge on each surface of the dielectric is Q'.
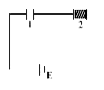
View SolutionTwo identical capacitors 1 and 2 are connected in series to a battery as pictured. Capacitor 2 has a dielectric slab of K constant. Q_(1) And Q_(2) , 1 and 2 have accumulated charges. Now, the dielectric slab is removed and the corresponding charge Q'_(1) And Q'_(2) If
View Solutionदो समरूप संधारित्र 1 एवं 2 को श्रेणी क्रम में बैटरी से चित्रानुसार जोड़ा गया है। संधारित्र 2 में एक परावैद्युत पट्टिका जिसका नियतांक K है जो की दिखाया गया है। Q1 एवं Q2 संधारित्र में संचित आवेश है। अब परावैद्युत पट्टिका को हटाया गया एवं क्रमागत आवेश Q1' एवं Q2' है तो-
View SolutionA dielectric slab is inserted between the plates of a capacitor. The charge on the capacitor is Q and the magnitude of the induced charge on each surface of the dielectric is Q'
View SolutionA parallel plate capacitor, each with plate area A and separation d is charged to a potential difference V. The battery used to charge it is then disconnected. A dielectric slab of thickness d and dielectric constant K is now place in the
charge on plates
View SolutionA parallel plate capacitor, each with plate area A and separation d is charged to a potential difference V. The battery used to charge it is then disconnected. A dielectric slab of thickness d and dielectric constant K is now place in the capacitance of the capacitor
View SolutionIf q_(f) is the free charge on the capacitor plates and q_(b) is the bound charge on the dielectric slab of dielectric constant k placed between the capacitor plates, then bound charge q_(b) can be expressed as :
View Solution
