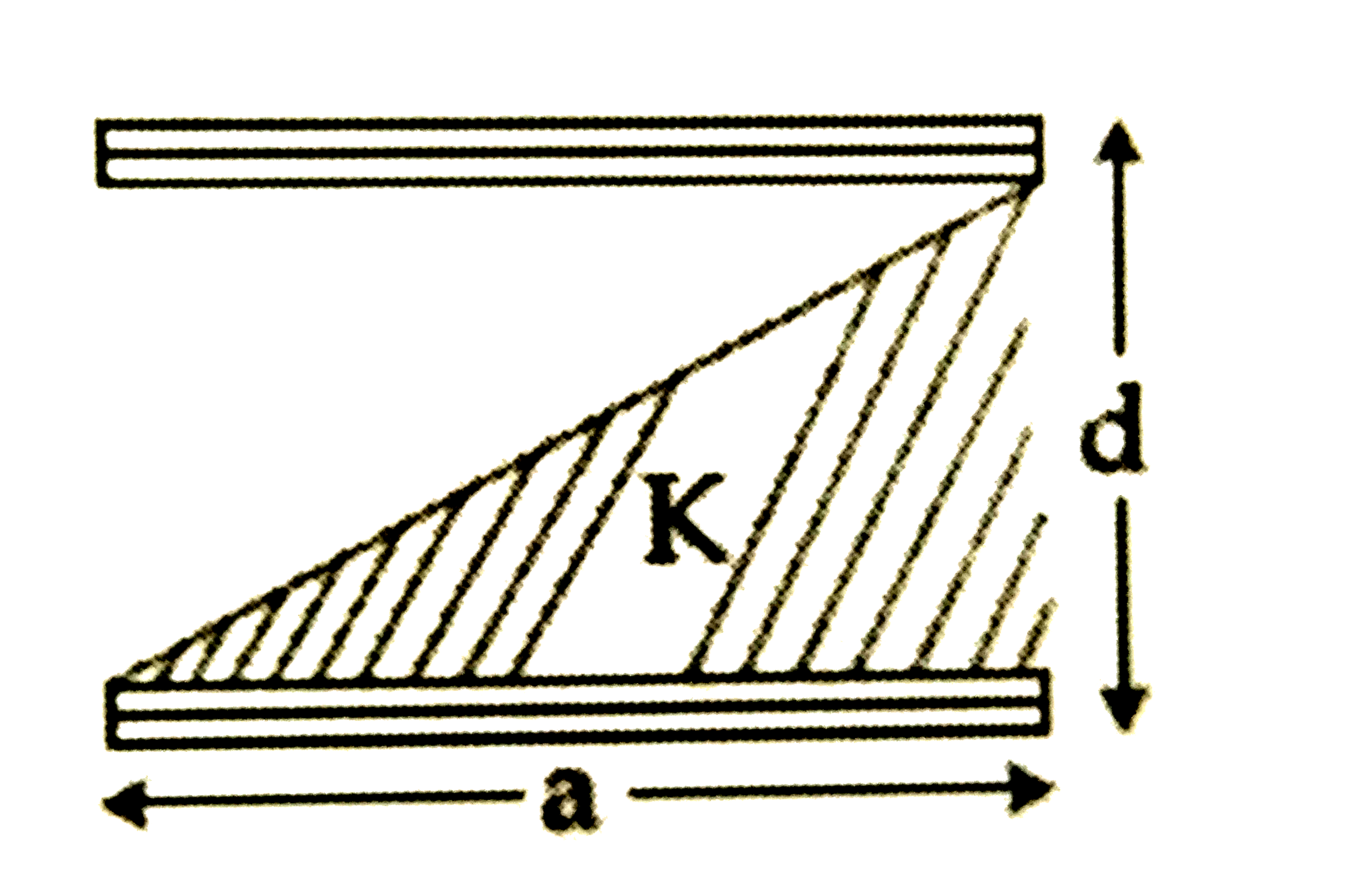
A paralled plate capacitor is made of two square plates of side 'a' , separated by a distance d (dltlta). The lower triangular portion is filled with a dielecttic of dielectric constant K, as shown in the figure. Capacitance of this Capacitor is :
The correct Answer is:C
Let.s consider a strip of thickness dx at a distance of x from the left end as shown in the figure.
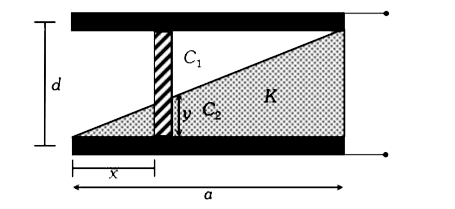
Now integrating it from 0 to a
Similar Questions
Figure shown a parallel-plate capacitor having square plates of edge a and plate-separation d. The gap between the plates is filled with a dielectric of dielectric constant K which varies parallel to an edge as where K and a are constants and x is the distance from the left end. Calculate the capacitance.

View SolutionA parallel plate capacitor is made of two square plates of side 'a' , separated by a distance d much less than a. The lower triangular portion is filled with a dielectric of dielectric constant K, as shown in the figure. Capacitance of this Capacitor is :
 a) K∈0a22d(K+1)
b) K∈0a2d(K−1)InK
c) K∈0a2dInK
d) 12K∈0a2d
a) K∈0a22d(K+1)
b) K∈0a2d(K−1)InK
c) K∈0a2dInK
d) 12K∈0a2d
View SolutionThe capacitor shown has square plates of side L and has gap d between the photos. In the dielectric constant of the materiale of the slab is k , the capacitance of the capacitor is

View SolutionA parallel plate capacitor with air as the dielectric has capacitance C. A slab of dielectric constant K and having the same thickness as the separation between the plates is introduced so as to fill one-fourth of the capacitor. The new capacitance will be
View SolutionA parallel plate capacitor, with plate area A and plate separation d, is filled with a dielectric slabe as shown. What is the capacitance of the arrangement ?
View SolutionA parallel plate capacitor of capacitance C (without dielectric) is filled by dielectric slabs as shown in figure. Then the new capacitance of the capacitor is

View SolutionA parallel plate capacitor with air as the dielectric has capacitance C. A slab of dielectric constant K and having the same thickness as the separation between plates is introduced so as to fill one-fourth of the capacitor as shown in the figure. The new capacitance will be :
View SolutionA parallel plate capacitor of area ‘A’ plate separation ‘d’ is filled with two dielectrics as shown. What is the capacitance of the arrangement ?

View Solution