A parallel plate capacitor of area A, plate separation d and capacitance C is filled with three different dielectric materials having dielectric constants , and as shown. If a single dielectric material is to be used to have the same capacitance C in this capacitor, then its dielectic constant k is given by
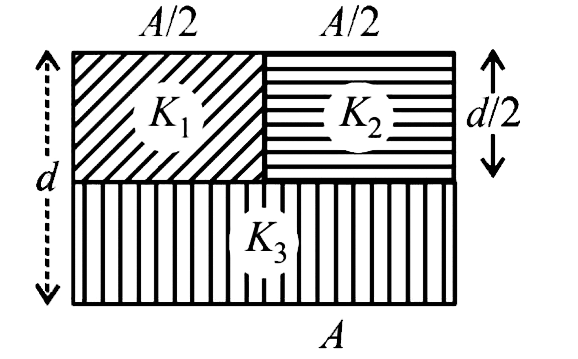
The correct Answer is:B
Similar Questions
A parallel plate capacitor has capacitance C. If it is equally filled with parallel layers of materials of dielectrics K1 and K2 —
View SolutionA parallel plate capacitor with air as the dielectric has capacitance C. A slab of dielectric constant K and having the same thickness as the separation between the plates is introduced so as to fill one-fourth of the capacitor. The new capacitance will be
View SolutionA parallel-plate capacitor of area A, plate separation d and capacitance C is filled with four dielectric materials having dielectric constants k1,k2,k3 and k4 as shown in the figure below. If a single dielectric material is to be used to have the same capacitance C in this capacitor, then its dielectric constant k is given by
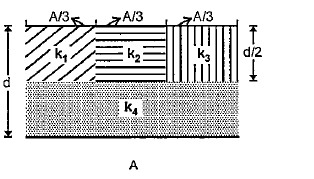
View SolutionA parallel plate capacitor of plate area A and separation d filled with three dielectric materials as show in figure. The dielectric constants are K_1 , K_2 and K_3 respectively. The capacitance across AB will be :
View SolutionA parallel plate capacitor with air as the dielectric has capacitance C. A slab of dielectric constant K and having the same thickness as the separation between plates is introduced so as to fill one-fourth of the capacitor as shown in the figure. The new capacitance will be :
View SolutionA parallel plate capacitor of area A, plate separation d and capacitance C is filled with three different dielectric materials having dielectric constants k_1 , k_2 and k_3 as shown. If a isngle dielectric material is to be used to have the same capacitance C in this capacitor, then its dielectic constant k is given by
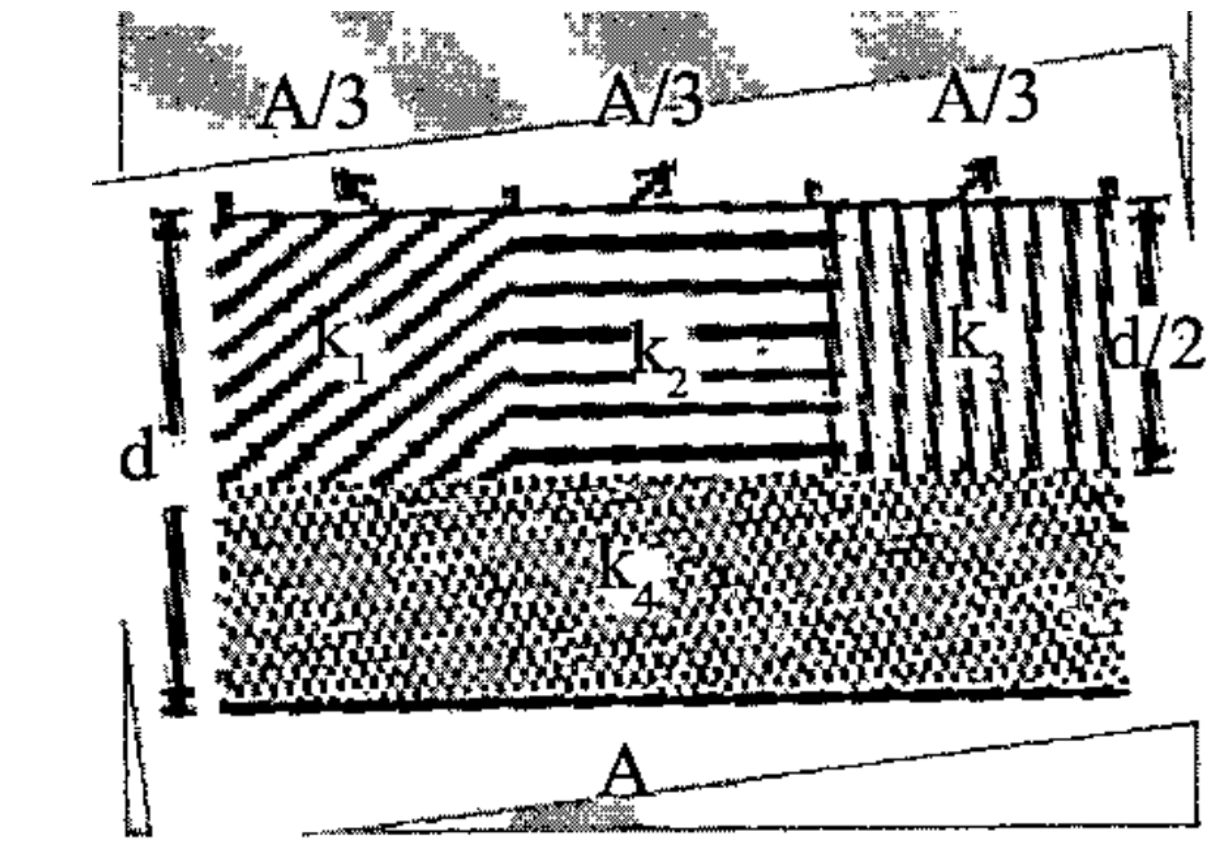
View SolutionA parallel-plate capacitor of area A,plate separation d and capacitance C is filled with foue dielectric matertials having dielectric constants k1,k2,k3 and k4 as shown in the figure below.If a single dielectric material is to be used to have the same capacitance C in this capacitor,then its dielectric constant k is given by
View SolutionA parallel of area A, plane separation d and capacitance C is filled with three diferent dielectric materials having constants k1,K2andk3 as shown. If a single dielectric material is to be used to have the same capacitance C in this capacitor, then its dielectric constant k is given by
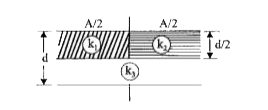
View Solution