a point charge q is situated at a distance r from one end of a thin conduction rod of length L having a charge Q (uniformly distributed a long its length).find the magnitudes of electric force between the two.
2KQr(r+L)
KQqr2
KQqr(r−L)
KQqr(r+L)
The correct Answer is:D
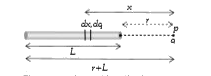
Charge on element length dx -
dq=(QL)dx
Force due to element charge dq and q –
dF=Kqdqx2
F=∫r+LrKq(Q/L)dxx
=KqQL[x−2x+1−2+1]L+rr=−KqQL[1x]L+rr
=−KqQL[1L+r−1r]⇒F=KQqr(L+r)
Similar Questions
A charge Q is uniformly distributed over a long rod AB of length L as in figure. The electric potential at the point 0 lying at a distance L from the end A is :

View SolutionFind the electric field at a point P on the perpendicular bisector of a uniformly charged rod. The length of the rod is L, the charge on it is Q and the distance of P from the centre of the rod is a.
View SolutionA point charge q is situated at a distance r from one end of a thin conduction rod of length L having a charge Q (uniformly distributed a long its length).find the magnitudes of electric force between the two.
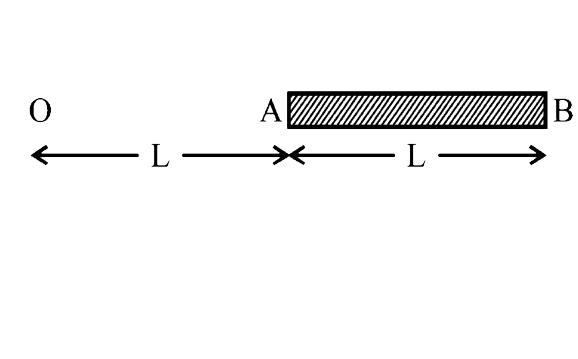
View SolutionA charge Q is uniformly distributed over a long rod AB of length L as shown in the figure. The electric potential at the point 0 lying at distance L from the end A is

View SolutionA thin straight rod of length l carrying a uniformly distributed charge q is located in vacuum. Find the magnitude of the electric force on a point charge 'Q' kept as shown in the figure.

View SolutionA charge Q is uniformly distributed over a long rod AB of length L as shown in the figure. The electric potential at the point O lying at distance L from the end A is
View SolutionA point charge 4 is situated at a distance r on axis from one end of a thin conducting rod of length L having a charge Q (Uniformly distributed along its length). "The magnitude of electric force between the two is ________.
View SolutionA point charge q is located at a distance d from one end of a thin non-conducting rod of length L on which the charge Q (distributed uniformly along the length) is, as shown in the figure. So the magnitude of the electric force between them is:
View Solution
