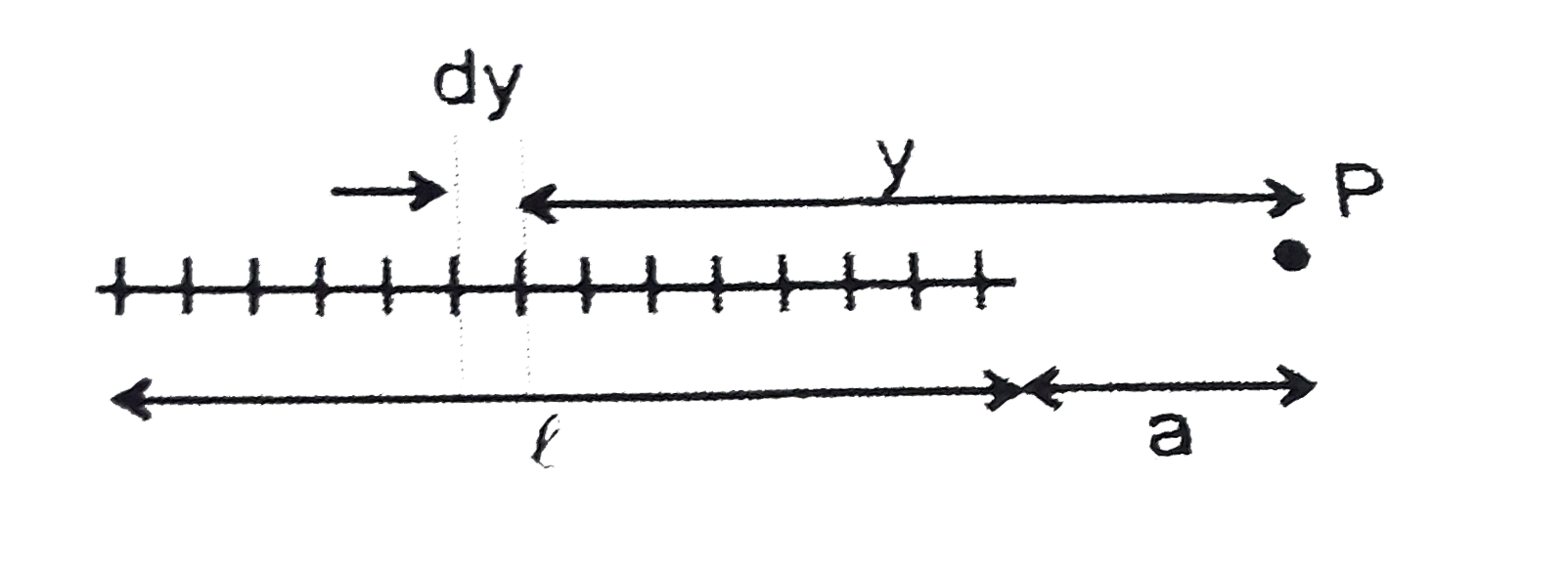
A thin straight rod of length l carrying a uniformly distributed charge q is located in vacuum. Find the magnitude of the electric force on a point charge 'Q' kept as shown in the figure.

As the charge on the rod is not point charge, therefore, first we have to find force on charge Q due to charge over a very small part on the length of the rod. This part, called element of length by can be considered as point charge.
Charge on element, dq=λdy=qldy
Electric force on 'Q' due to element
=K.dq.Qy2=K.Q.q.dyy2.l
All force are along the same direction,
∴F=∑dF. This sum can be calculated using integration,
therefore, F=a+l∫y=aKQqdyy2l=KqQl=[−1y]a+la=KQ.ql[1a−1a+l]=KQqa(a+l).
Topper's Solved these Questions
- ELECTROSTATICSBook:RESONANCEChapter:ELECTROSTATICSExercise:Problems
Explore 22 Videos
- ELECTROSTATICSBook:RESONANCEChapter:ELECTROSTATICSExercise:Exercise-1 Section (A)
Explore 9 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCEChapter:ELECTROMAGNETIC INDUCTIONExercise:A.l.P
Explore 19 Videos
- EXPERIMENTAL PHYSICSBook:RESONANCEChapter:EXPERIMENTAL PHYSICSExercise:PART -II
Explore 10 Videos
Similar Questions
A thin straight rod of length 2a carrying a uniformly distributed charge q is located in vacumm. Find the magnitude of the electric field strength as a function of the distatance r from the rod's centre along the streaight line
(a) perpendicular to the rod and passing through its centre ,
(b) coinciding with the rod's direction (at the point lying outside the rod).
View Solutiona point charge q is situated at a distance r from one end of a thin conduction rod of length L having a charge Q (unifromly distributed a long its length).find the magnitudes of electric froce between the two.
View Solution
Knowledge Check
A rod of length l having uniformly distributed charge Q is rotated about one end with constant frequency f Its magnetic moment
AπfQl2BπfQl23C2πfQl23D2πRQ2A 10 cm long rod carries a charge of +150μC distributed uniformly along its length. Find the magnitude of the electric field at a point 10 cm from both the ends of the rod.
A15.6×107N/CB15.6×105N/CC1.56×107N/CD1.56×105N/CA cube is made from six thin insulating square faces, each square having side 'd' and carrying a uniformly distributed charge of Q. The magnitude of electric flux leaving the sixth face, due to the electric field of other five faces, is φ. The magnitude of electrostatic force on each face of cube is F. Then,
Aφ=5Q6E0Bφ=Q2E0CF=2Q2E0d2DF=Q2E0d2
A point charge q is located at the centre fo a thin ring of radius R with uniformly distributed charge −q, find the magnitude of the electric field strength vectro at the point lying on the axis of the ring at a distance x from its centre, if x>>R.
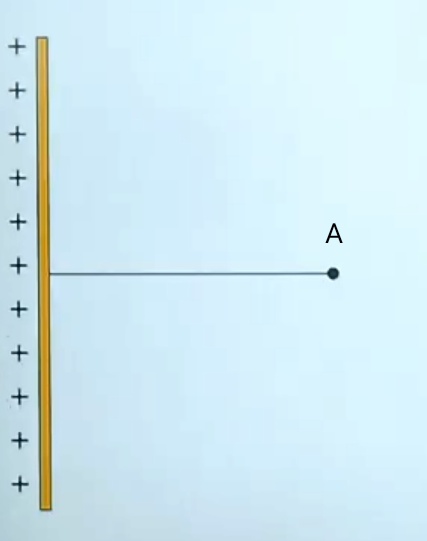
View SolutionA wire of length L carries charge Q uniformly distributed along its length. Find the electric field at a distance √3L2 from the wire at point A as shown.
View SolutionA rod length l is uniformly charged with charge q. Calculate potential at point P.

View SolutionFigure 22-24 shows a plastic rod having a uniformly distributed charge. The charge per unit length of the rod is λ. Find the electric field due to the rod at a point P which is at a distance r from the rod.
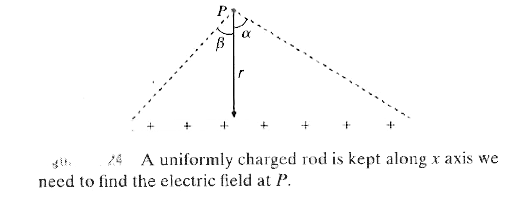
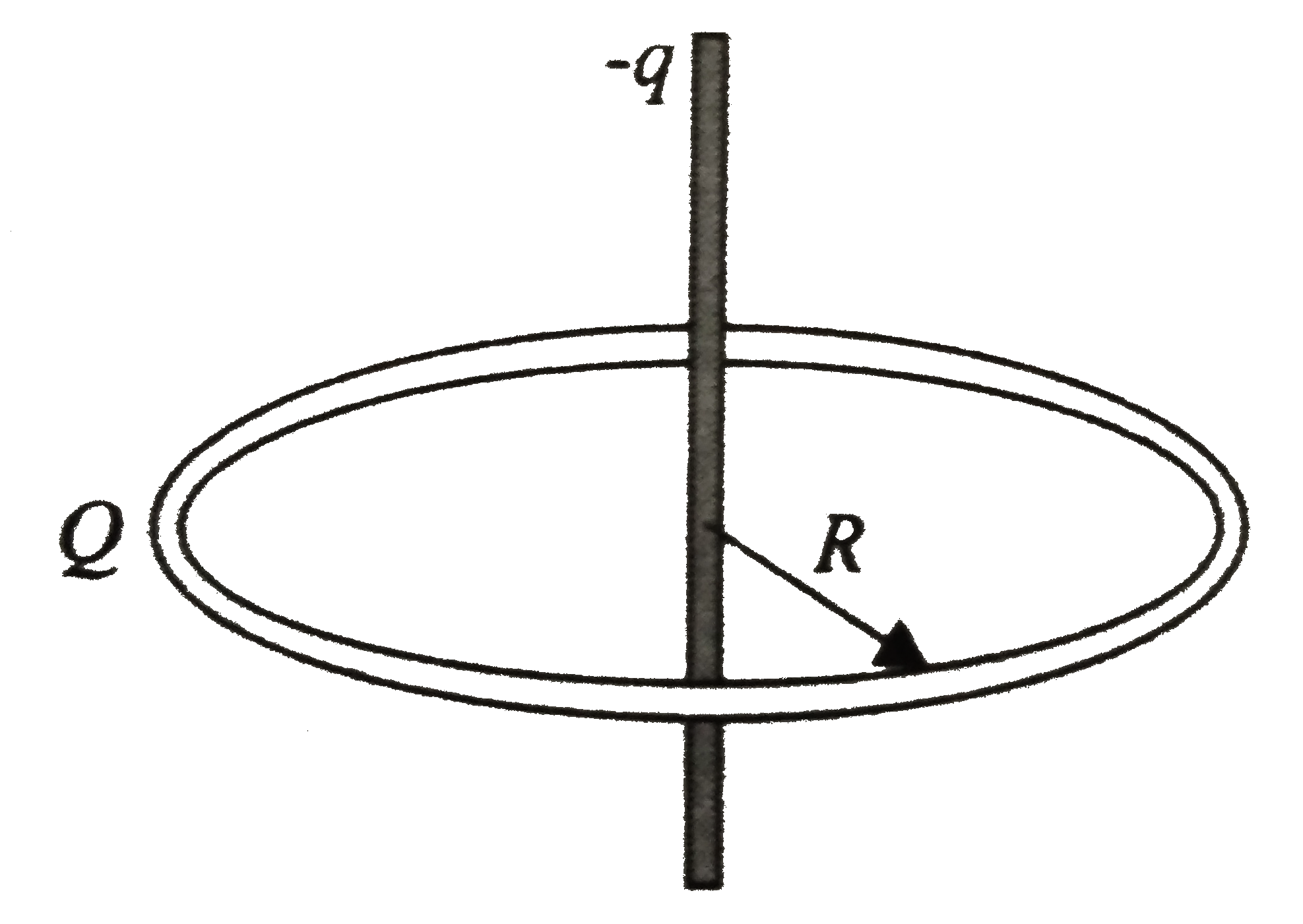
View SolutionIn a free space, a thin rod carrying uniformly distributed negative charge −q is placed symmetrically along the axis of a tin ring of radius R varrying uniformly dostributed charge Q. The mass of the rod is m and length is l=2R. The ring is fixed and the rod is free to move. The rod is displaced slightly along the axis of the ring and then released. Find the period T to the small amplitude oscillations of the rod.
View Solution

