A simple harmonic motion is represented by : $y = 5 (sin 3 π t + \sqrt{3} cos 3 π t) c m$ The amplitude and time period of the motion are :

A

$5 c m \frac{2}{3} s$

B

$10 c m \frac{3}{2} s$

C

$10 c m \frac{2}{3} s$

D

$5 c m \frac{3}{2} s$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

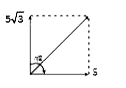
$y = 5 sin (3 π t) + 5 \sqrt{3} cos 3 π t 5 \sqrt{3}$
$ω = 3 π$
$T = \frac{2 π}{ω} = \frac{2}{3} sec$

|

Updated on:21/07/2023

Class 11 PHYSICS SIMPLE HARMONIC MOTION

Similar Questions

Which of the following functions of time represent (a) simple harmonic, (b) periodic but not simple harmonic, and (c) non-periodic motion? Give period for each case of periodic motion ( $ω$ is any positive constant):
(a) $sin ω t - cos ω t$
(b) ${sin}^{3} ω t$
(c) $3 cos (π / 4 - 2 ω t)$
(d) $cos ω t + cos 3 ω t + cos 5 ω t$
(e) $exp (- ω^{2} t^{2})$
(f) $1 + ω t + ω^{2} t^{2}$
05:10
View Solution
Two simple harmonic motions are represented by y_(1) = 10 sin"" (pi)/(4) (12t+1)" and " y_(2) = 5(sin"" 3pi t+ sqrt(3) cos 3pi t) . Find out the ratio of their amplitudes. What are the time period of two motions.
04:02
View Solution
Show that the motion of a particle represented by $y = sin ω t - cos ω t$ is simple harmonic with a period of $\frac{2 π}{ω}$ .
02:17
View Solution
A simple harmonic motion is represented by : y=5(sin3pit+sqrt(3)cos3pit)cm The amplitude and time period of the motion by :
03:10
View Solution
Two SHM are represented by the equations y_(1) = 10 sin(3pi t + pi//4) and y_(2) = 5[sin 3pi t + sqrt(3) cos 3pi t] . Their amplitudes are in the ratio
02:26
View Solution
Which of the following functions of time represent (a) simple harmonic motion and b. periodic but not simple harmonic? Give the period for each case. (1) sin omega t -cos omega t 2. sin^(2)omega t
View Solution
Which of the following functions of time represent (a) simple harmonic motion and b. periodic but not simple harmonic? Give the period for each case.
(1) $sin ω t - cos ω t$ 2. ${sin}^{2} ω t$
View Solution
Two harmonic motions are represented by the equations $y_{1} = 10 sin (3 π t + \frac{π}{4})$
$y_{2} = 5 (sin 3 π t + \sqrt{3} cos 3 π t)$
their amplitudes are in the ratio
03:36
View Solution

Recommended Questions

Home
Ask Doubt
Profile