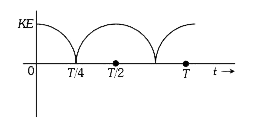
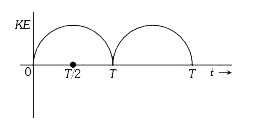
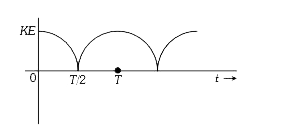
A particle is executing simple harmonic motion with a time period . At time it is at its position of equilibium. The kinetice energy -time graph of the particle will look like

The correct Answer is:A
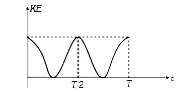
Note : But as per options given, best possible answer will be option (a)
Similar Questions
A particle is executing simple harmonic motion with a time period T. At time t=0, it is at its position of equilibium. The kinetice energy -time graph of the particle will look like
View SolutionA particle is excuting simple harmonic motion with an amplitude A and time period T. The dispolacement of the particle after 2 T period from its intial position is,
View SolutionA particle is excuting simple harmonic motion with an amplitude A and time period T. The dispolacement of the particle after 2 T period from its intial position is,
View SolutionA particle is executing simple harmonic motion with an amplitude A and time period T. The displacement of the particles after 2T period from its initial position is
View SolutionA particle executing simple harmonic motion with time period T. the time period with which its kinetic energy oscillates is
View SolutionA particle is executing simple harmonic motion with an amplitude A and time period T. The displacement of the particles after 2T period from its initial position is
View SolutionA particle is executing simple harmonic motion with a time period T. At time t=0, it is at its position of equilibium. The kinetice energy -time graph of the particle will look like
View SolutionIf particle is excuting simple harmonic motion with time period T, then the time period of its total mechanical energy is :-
View Solution