A small mass m attached to one end of a spring with a negligible mass and an unstretched length L, executes vertical oscillations with angular frequency ω0. When the mass is rotated with an angular speed ω by holding the other end of the spring at a fixed point, the mass moves uniformly in a circular path in a horizontal plane. Then the increase in length of the spring during this rotation is
ω2Lω20−ω2
ω20Lω2−ω20
ω2Lω20
ω20Lω2
The correct Answer is:A
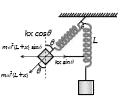
kxsinθ=mω2(L+x)sinθ
⇒kx=mω2(L+x)
Since, ω0=√km
k=mω20
mω20x=mω2(L+x)
⇒x=ω2Lω20−ω2.
Similar Questions
A small mass m attached to one end of a spring with a negligible mass and an unstretched length L, executes vertical oscillations with angular frequency ω0 When the mass is rotated with an angular speed ω by holding the other end of the spring at a fixed point, the mass moves uniformly in a circular path in a horizontal plane. Then the increase in length of the spring during this rotation is
View SolutionA small mass m attached to one end of a spring with a negligible mass and an unstretched length L, executes vertical oscilllations with angular frequency ω0. When the mass is rotated with an angular speed ω by holding the other end of the spring at a fixed point, the mass moves uniformly in a circular path in a horizontal plane. Then the increase in length of the spring during this rotation is
View Solutiona mass m is suspended at one end of a spring and the other end of the spring is fimly fixed on the celling. if the mass is slightly depressed and released it will execute oscillation. write down the expression for the frequency of oscillation of the mass.
View SolutionIn a spring- mass system , the length of the spring is L, and it has a mass M attached to it and oscillates with an angular frequency ω. The spring is then cut into two parts, one (i) with relaxed length αL and the other (ii) with relaxed length (1−α) L. The force constants of the two spring A and B are
View Solutionm द्रव्यमान के एक कण को असकुंचित l लम्बाई, k स्प्रिंग नियतांक वाली हल्की स्प्रिंग के एक सिरे से जोड़ा जाता है। अब निकाय को स्प्रिंग के दूसरे सिरे के सापेक्ष ω कोणीय चाल से नगण्य गुरुत्व क्षेत्र में घुमाया जाता है। स्प्रिंग में विस्तार होगा (मानिए कि दोलन नहीं होता है )-

View Solution"A mass is attached to one end of a spring and by holding the other end in hand, the spring is whirled in a horizontal circle" What happens to the length of the spring ?
View SolutionAn underformed spring with the spring constant k has length l_(0) . When the system (Fig.) rotates at an angular velocity omega , the weight with mass m causes an extension of the spring. Find the length l of the rotating spring.
View Solutionm द्रव्यमान का एक कण k बल नियतांक और । अतानित लंबाई की एक हल्की स्प्रिंग के एक सिरे पर कसा हुआ है। निकाय को गुरुत्वाकर्षण मुक्त समष्टि में, ωकोणीय वेग के साथ स्प्रिंग के दूसरे सिरे के परितः घुमाया जाता है। तब स्प्रिंग की लंबाई में कितनी वृद्धि होगी?
View Solution
