Two identical spring of constant K are connected in series and parallel as shown in figure. A mass is suspended from them. The ratio of their frequencies of vertical oscillations will be 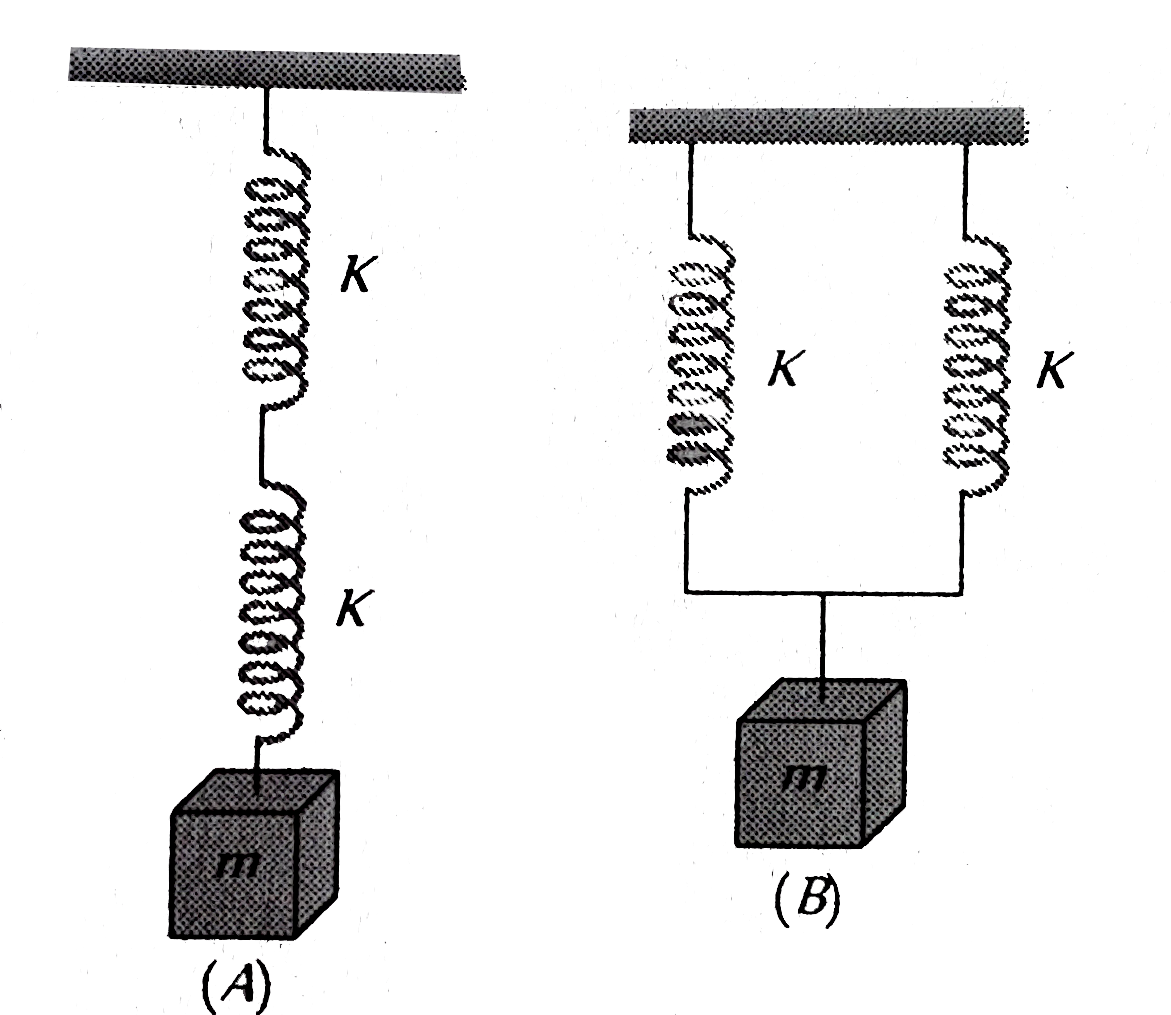
2:1
1:1
1:2
4:1
The correct Answer is:A
(A) Keq=kk2k=k2
T1=2π√mk/2⇒1f1=2π√k2m
(B) Keq=2k
T2=2π√m2k⇒1f2=2π√2km
f1f2=21.
Similar Questions
Two spring of force constants k and 2k are connected to a mass as shown in figure. The frequency of oscillation of the mass is……..

View SolutionTwo identical springs of spring constant k each are connected in series and parallel as shown in figure. A mass M is suspended from them. The ratio of their frequencies of vertical oscillation will be
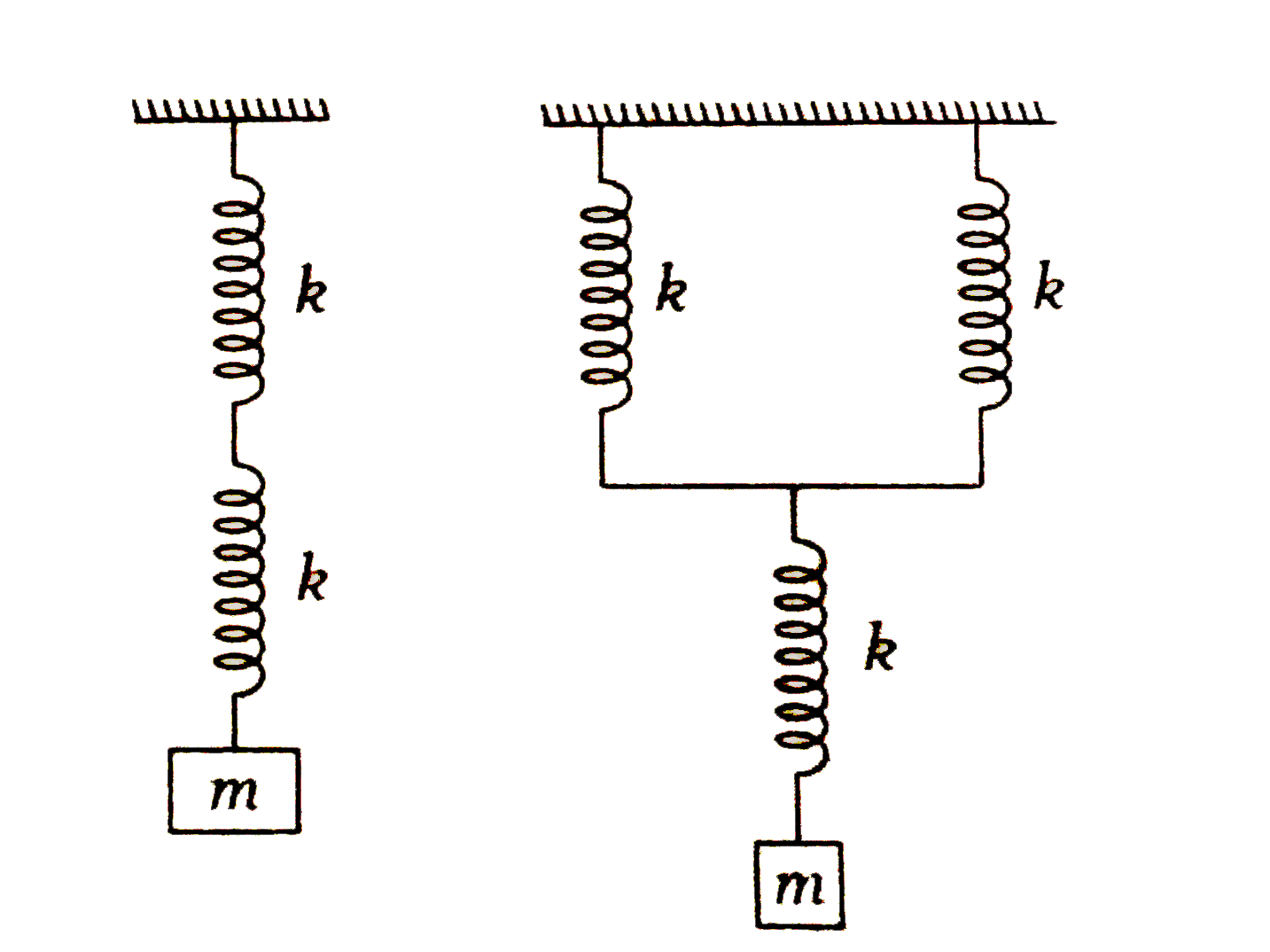
View SolutionSome springs are combined in series and parallel arrangement as shown in the figure and a mass m is suspended from them. The ratio of their frequencies will be
View SolutionTwo identical springs, each of spring constant K, are connected first series and then in parallel. A mass M is suspended from them. The ratio of the frequencies of vertical oscillations will be :
View SolutionTwo identical springs of constant k are connected , first in series and then in parallel. A matal block of mass m is suspended from their combination. The ratio of their frequencies of vertical oscillations will be in a ratio
View SolutionSome springs are combined in series and parallel arrangement as shown in the figure and a mass m is suspended from them. The ratio of their frequencies will be :-
_E01_040_Q01.png)
View SolutionTwo identical spring of constant K are connected in series and parallel as shown in figure. A mass is suspended from them. The ratio of their frequencies of vertical oscillations will be
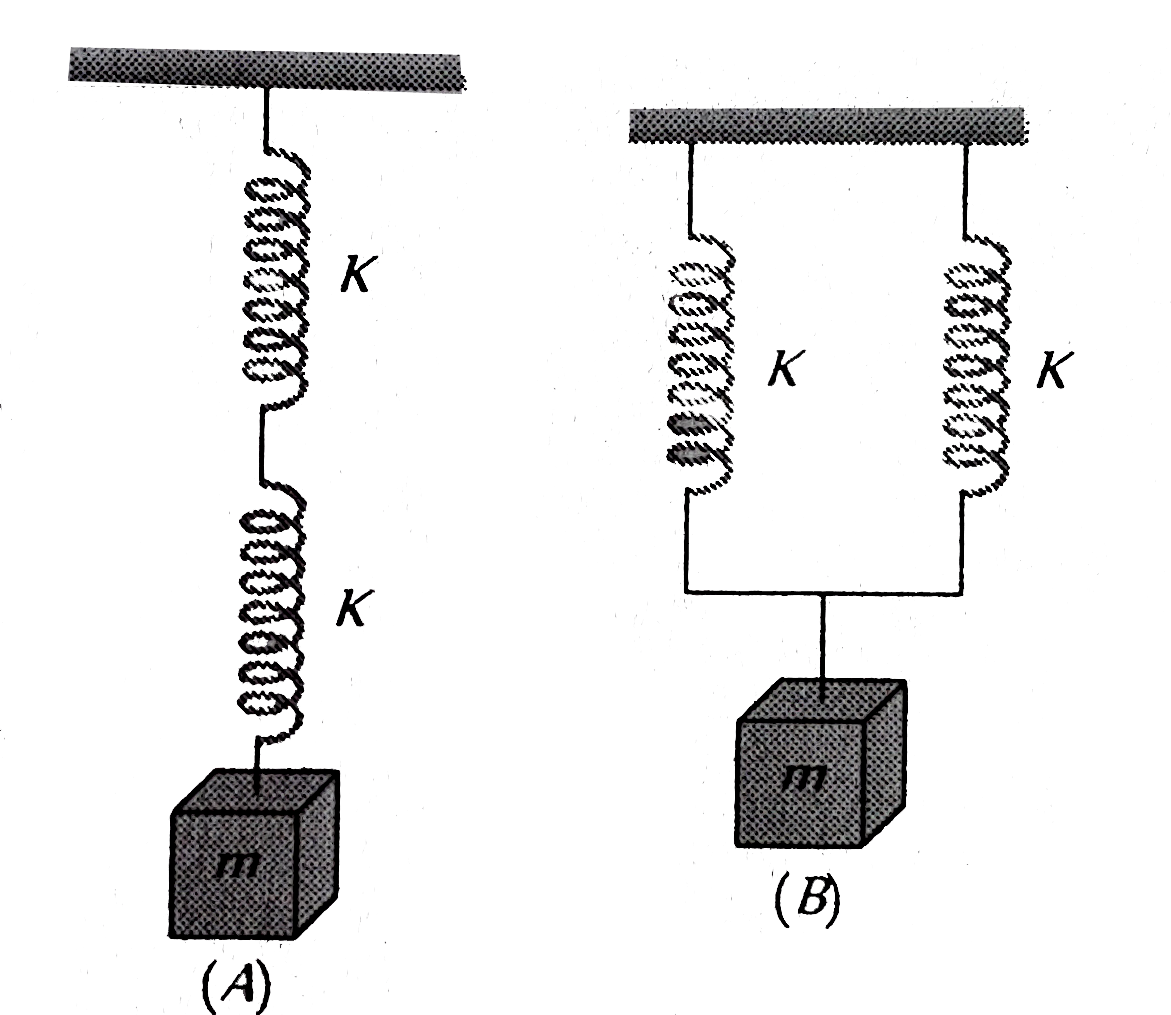
View SolutionTwo identical spring of constant K are connected in series and parallel as shown in figure. A mass is suspended from them. The ratio of their frequencies of vertical oscillations will be
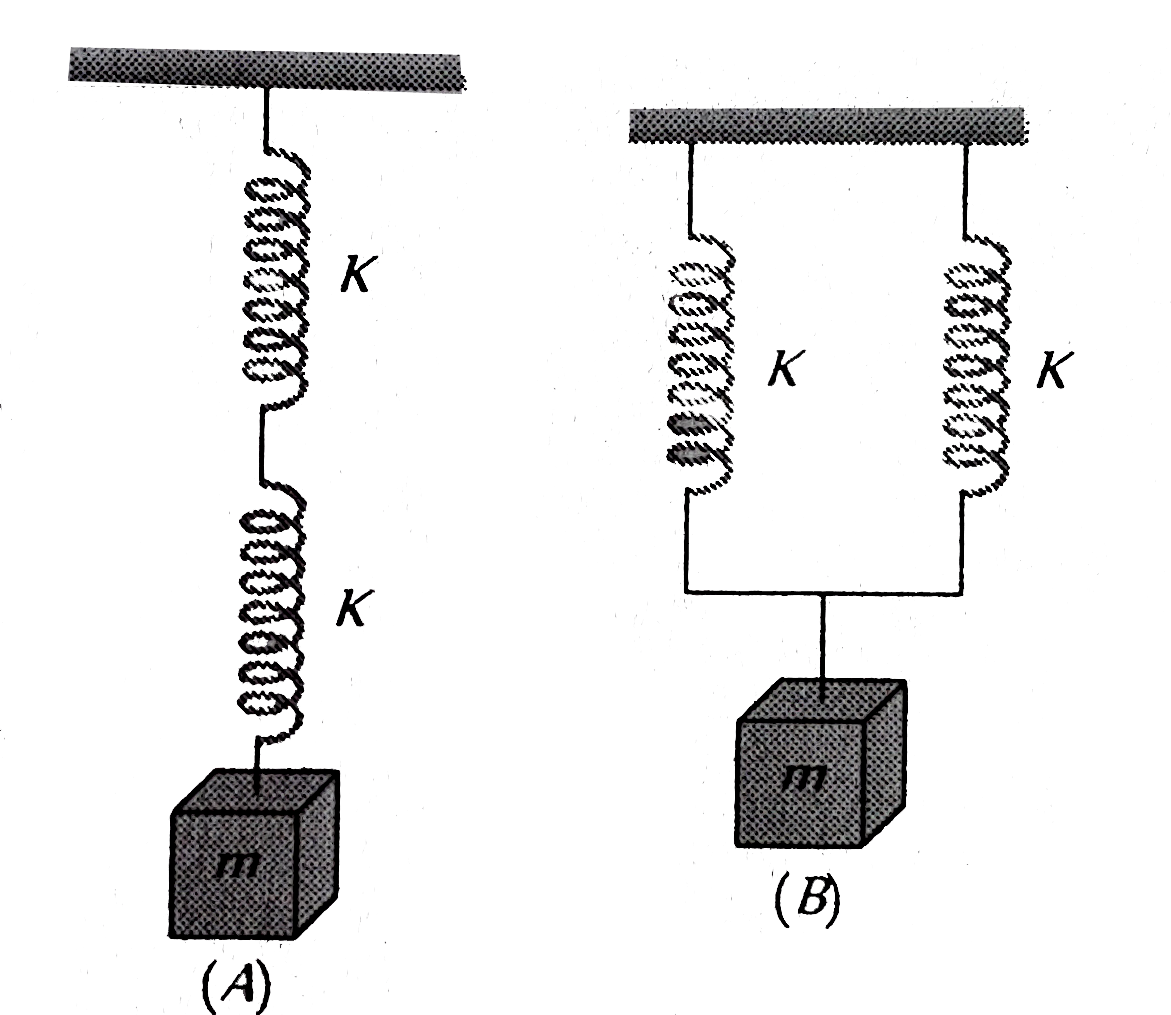
View Solution