Find the ratio of the periods of two identical springs if they are fir

Two identical capacitors are first connected in series and then in parallel. The ratio of equivalent capacitance is
A $1 : 1$
B $1 : 2$
C $1 : 3$
D $1 : 4$
Two identical springs of spring constant k each are connected in series and parallel as shown in figure. A mass M is suspended from them. The ratio of their frequencies of vertical oscillation will be

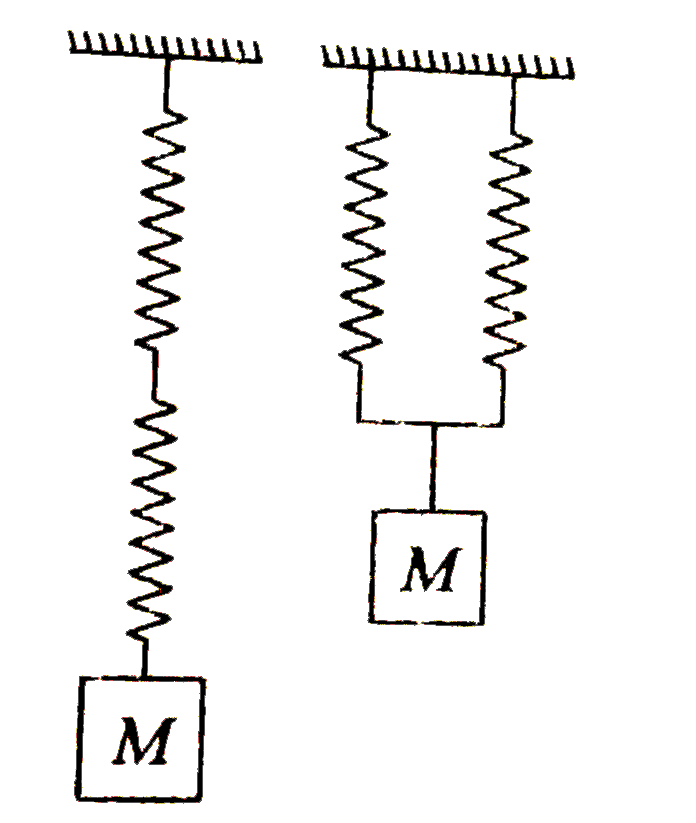A $1 : 2$
B $2 : 1$
C $4 : 1$
D $1 : 4$
Let $T_{1} and T_{2}$ be the periods of springs A and B when mass M is suspended from one end of each spring. If both springs are taken in series and the same mass A is, suspended from the séries combination, the time period is T, then
A $T = T_{1} + T_{2}$
B $\frac{1}{T} = \frac{1}{T_{1}} + \frac{1}{T_{2}}$
C $T^{2} = T_{1}^{2} + T_{2}^{2}$
D $\frac{1}{T^{2}} = \frac{1}{T_{1}^{2}} + \frac{1}{T^{2}}$

Find the ratio of the periods of two identical springs if they are first joined in series & then in parallel & a mass $m$ is suspended from them: