The variation of potential enegy of harmonic oscillator is as shown in figure. The spring constant is
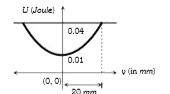
The correct Answer is:B
Resting PE=0.01 J
Maximum KE=0.04-0.01=0.03 J
.
Similar Questions
The variation of the potential energy of harmonic oscillator is as shown in the figure. The spring constant is
View SolutionThe change in potential energy of a simple rotating oscillator is shown in the figure, the force constant will be.
View SolutionA simple harmonic motion oscillator has two springs of spring constant k and other two of spring constant 2k, arranged as shown in the figure. Calculate the time period of oscillator.
View Solutionचित्र में दिखाई गई स्प्रिंगों के दोलनों की आवृति होगी
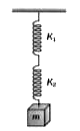
View SolutionThe variation of PE of a simple harmonic oscillator is as shown. Then force constant of the system is (PE 'U' is in joules, displacement 'x' is in mm)

View SolutionA system of springs with their spring constants are as shown in figure. What is the frequency of oscillations of the mass m ?
View SolutionThe velocity-time diagram of a harmonic oscillator is shown in the adjoining figure . The frequency of oscillation is
View SolutionAs shown in figure, a simple harmonic motion oscillator having identical four springs has time period
View Solution