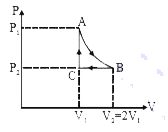
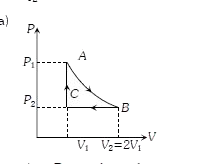
n mole a perfect gas undergoes a cyclic process ABCA (see figure) consisting of the following processes.
: Isothermal expansion at temperature T so that the volume is doubled from to and pressure changes from to
: Isobaric compression at pressure to initial volume
: Isochoric change leading to change of pressure from to .
Total work done in the complete cycle ABCA is :
0
The correct Answer is:A
= isothermal process
= isobaric process
isochoric process
Also,
Work done by gas in the complete cycle ABCA is
, as isochoric process
ln ln(2)
Now put the value of in equation, we get,
ln (2)
Similar Questions
Initially a gas of diatomic molecules is contained in a cylinder of volume V_1 at a pressure P_1 and temperature 250 K. Assuming that 25% of the molecules get dissociated causing a change in number of moles. The pressure of the resulting gas, at temperature 2000 K, when contained in a volume 2V_1 is given by P_2 . The ratio P_2//P_1 is ________.
View SolutionAn ideal gas expands isothermally from a volume V_1 to V_2 and then compressed to original volume V_1 adiabatically. Initial pressure is P_1 and final pressure is P_3 . The total work done is W. Then.
View Solutionn mole a perfect gas undergoes a cyclic process ABCA (see figure) consisting of the following processes.
A→B: Isothermal expansion at temperature T so that the volume is doubled from V1 to V2=2V1 and pressure changes from P1 to P2
B→C : Isobaric compression at pressure P2 to initial volume V1
C→A : Isochoric change leading to change of pressure from P2 toP1 .
Total work done in the complete cycle ABCA is :

View SolutionAn ideal gas is initially at P1,V1 is expands to P2,V2 isothermally and then compressed adiabatically to the same volume V1 and pressure P3. If W is the net work done by the gas in complete process which of the following is true.
View SolutionWhat is an isothermal process? State essential conditions for such a process to take place. Show analytically that work done by one mole of an ideal gas during isothermal expansion from volume V1 to volume V2 is given by =RT logeV2V1 . What is the change in internal energy of a gas, which is compressed isothermally?
View SolutionAn ideal gas is initially at P1,V1 is expands isothermally to P2,V2 and then compressed adiabatically to the same volume V1 and pressure P3. If W is the net work done by the gas in complete process which of the following is true.
View SolutionAn ideal gas undergoes isobaric expansion at pressure P from volume V_1 to V_2 the work done is :
View SolutionAn ideal monatomic gas undergoes a cyclic process ABCA as shown in the figure. Graph of pressure versus volume of the cyclic process ABCA is
View Solution