Ideal gas undergoes an adiabatic change in its state from (P1V1,T1) to(,P2,V2T2). The work done (W) in the process is (n = number of moles, Cp and Cv are molar specific heats of gas)
W=n(T1−T2)CP
W=n(T1−T2)Cv
W=n(T1+T2)Cp
W=n(T1+T2)CV
The correct Answer is:B
To find the work done (W) during an adiabatic process for an ideal gas transitioning from state (P1,V1,T1) to (P2,V2,T2), we can follow these steps:
1. Understand the Adiabatic Process: In an adiabatic process, there is no heat exchange with the surroundings. This means that the change in internal energy (ΔU) is equal to the work done on or by the system.
ΔU=W
2. Use the First Law of Thermodynamics: The first law of thermodynamics states that:
ΔU=Q−W
Since Q=0 for an adiabatic process, we have:
ΔU=−W⇒W=−ΔU
3. Calculate the Change in Internal Energy: The change in internal energy for an ideal gas can be expressed as:
ΔU=nCv(T2−T1)
where n is the number of moles, and Cv is the molar specific heat at constant volume.
4. Substituting into the Work Done Equation: Substitute the expression for ΔU into the work done equation:
W=−nCv(T2−T1)
5. Rearranging the Equation: This can be rearranged to show that:
W=nCv(T1−T2)
6. Final Expression: The work done by the gas during the adiabatic process can thus be expressed as:
W=nCv(T1−T2)
Topper's Solved these Questions
- THE FIRST LAW OF THERMODYNAMICSBook:RESNICK AND HALLIDAYChapter:THE FIRST LAW OF THERMODYNAMICSExercise:PRACTICE QUESTIONS ( MORE THAN ONE CORRECT CHOICE TYPE )
Explore 9 Videos
- THE FIRST LAW OF THERMODYNAMICSBook:RESNICK AND HALLIDAYChapter:THE FIRST LAW OF THERMODYNAMICSExercise:PRACTICE QUESTIONS ( LINKED COMPREHENSION )
Explore 15 Videos
- THE FIRST LAW OF THERMODYNAMICSBook:RESNICK AND HALLIDAYChapter:THE FIRST LAW OF THERMODYNAMICSExercise:PROBLEMS
Explore 41 Videos
- TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION Book:RESNICK AND HALLIDAYChapter:TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION Exercise:PRACTICE QUETIONS (Integer Type)
Explore 4 Videos
- THE KINETIC THEORY OF GASESBook:RESNICK AND HALLIDAYChapter:THE KINETIC THEORY OF GASESExercise:PRACTICE QUESTIONS
Explore 72 Videos
Similar Questions
Assertion: When ideal gas expand from P1,V1,T1, to P2,V2,T2 two steps, and work done is high in which number of steps are high
Reason: Work is path function
View SolutionOne mole of a gas in the state A(P1,V1,T1) is subjected to adiabatic expansion to attain state B(P2,V2,T2). The work done by the gas is:
View Solution
Knowledge Check
The work done in changing the state from (P0,V0) to (P1,V1) in the following system is :
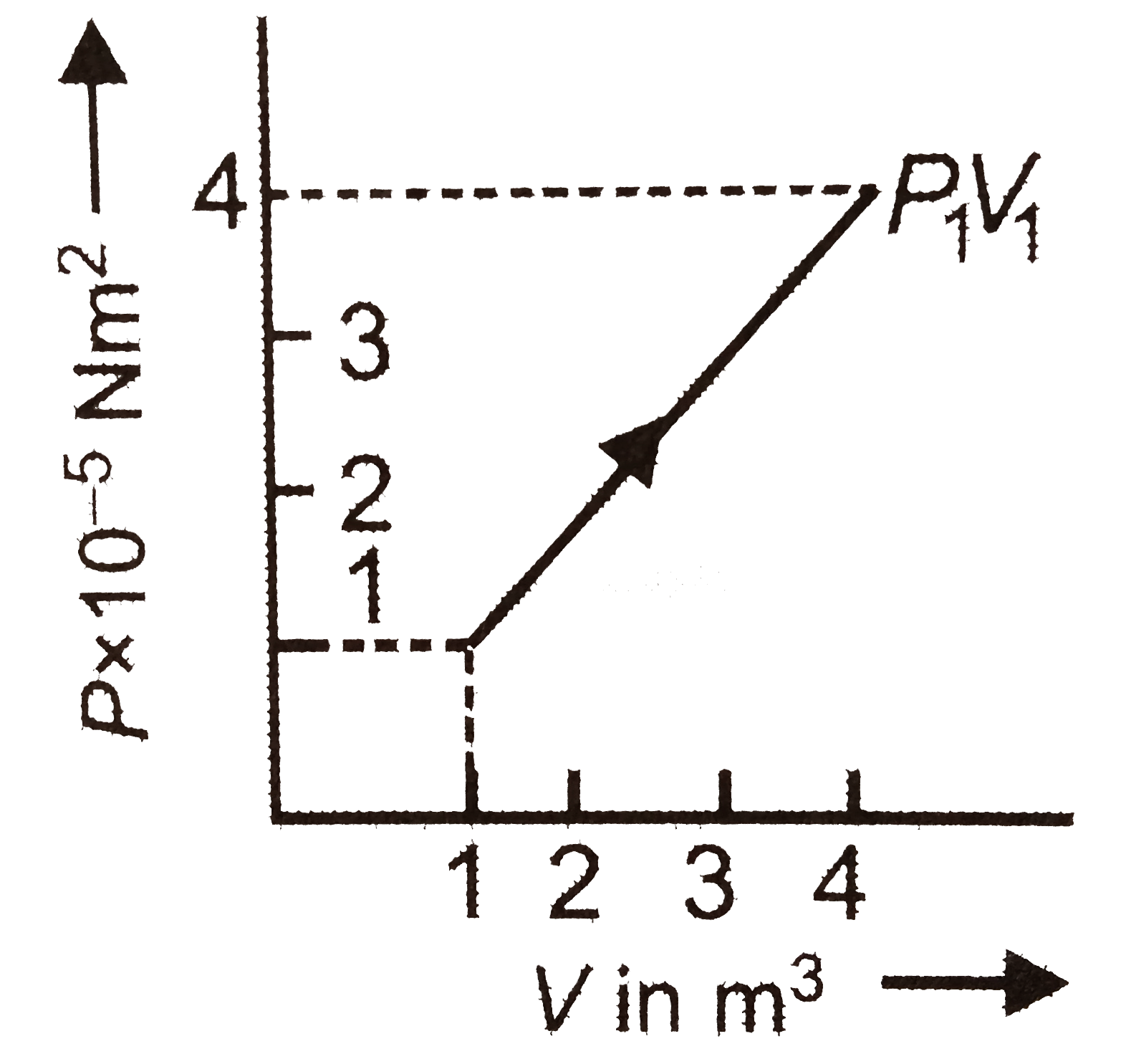 A−7.5×10−5JB−7.5×105JC−7.5×105ergD−7.5×10−5 erg
A−7.5×10−5JB−7.5×105JC−7.5×105ergD−7.5×10−5 ergA gas expands under constant pressure P from volume V1 toV2The work done by the gas is
AP(V2−V1)BP(V1−V2)CP(Vλ1−Vλ2)DPV1V2V2−V1In an adiabatic process, the state of a gas is changed from P1,V1,T1,toP2,V2,T2. Which of the following relation is correct
AT1Vλ−11=T2Tλ−12BP1Vλ−11=P2Vλ−12CT1Pλ1=T2Pλ2DT1Vλ1=T2Vλ2
One mole of hydrogen, assumed to be ideal, is adiabatically expanded from its initial state (P1,V1,T1) to the final state (P2,V2,T2). The decrease in the internal energy of the gas during this process will be given by
View SolutionAn ideal gas follows a process described by PV2=C from (P1,V1,T1) to (P2,V2,T2) (C is a constant). Then
View SolutionA gaseous system changes from state A(P1,V1,T1) to B(P2,V2,T2), B to C (P3,V3T3) and finally from C to A. The whole process may be called
View SolutionA gaseous system changes from state A(P1,V1,T1) to B(P2,V2,T2) to C(P3,V3,T3) and finally from C to A. The whole process may be called :
View SolutionAn ideal gas is transformed from state A(P1,V1) to the state B(P2,V2) through path AB. In this process the work done by the gas is
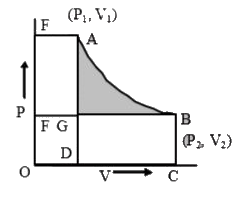
View Solution

