The change in the entropy of a 1 mole of an ideal gas which went through an isothermal process form an initial state (P1,V1,T) to the final state (P2,V2,T) is equal to
Zero
R In T
R In V1V2
R In V1V1
The correct Answer is:D
Change in entropy of an ideal gas -
ΔS=ΔQT
For isothermal process ΔU=0 Now, ΔQ=ΔU+ΔW⇒ΔQ=ΔW
ΔQ=ΔW=nRTIn(V2V1)
for n = 1 (one mole) ΔS=ΔQT=RIn(V2V1)
Similar Questions
Ideal gas undergoes an adiabatic change in its state from (P1V1,T1) to(,P2,V2T2). The work done (W) in the process is (n = number of moles, Cp and Cv are molar specific heats of gas)
View SolutionOne mole of gas obey the equation of state P(V - b) = RT and changes its coordinate from (P_1, V_1) to (P_2, V_2) which is established on P-V diagram by line. The work done in this changes will be _____
View SolutionIdeal gas undergoes an adiabatic change in its state form (P1,V1,T1) to (P2,V2,T2) . The work done W in the process is :
View Solutionn mole a perfect gas undergoes a cyclic process ABCA (see figure) consisting of the following processes.
A→B: Isothermal expansion at temperature T so that the volume is doubled from V1 to V2=2V1 and pressure changes from P1 to P2
B→C : Isobaric compression at pressure P2 to initial volume V1
C→A : Isochoric change leading to change of pressure from P2 toP1 .
Total work done in the complete cycle ABCA is :
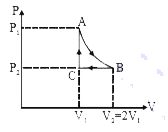
View SolutionA system changes from the state ( P_1,V_1 ) to ( P_2,V_2 ) as shown in the figure, what is the work done by the system?
View SolutionAn ideal gas is initially at P1,V1 is expands to P2,V2 isothermally and then compressed adiabatically to the same volume V1 and pressure P3. If W is the net work done by the gas in complete process which of the following is true.
View SolutionA gas is expanded from its initial state (Pressure P1 Volume V1) to its final state (V2) in isothermally. In case of which the final pressure will be more and the work done will be more? Explain your answer.
View SolutionWhat is an isothermal process? State essential conditions for such a process to take place. Show analytically that work done by one mole of an ideal gas during isothermal expansion from volume V1 to volume V2 is given by =RT logeV2V1 . What is the change in internal energy of a gas, which is compressed isothermally?
View Solution