An ideal gas follows a process described by PV2=C from (P1,V1,T1) to (P2,V2,T2) (C is a constant). Then
If P1>P2 then T2>T1
If V2>V1 then T2<T1
If V2>V1 then T2>T1
If P1>P2 then V1>V2
The correct Answer is:B
PV2=C⇒(nRTV)V2=C
⇒TV=C⇒T1V1=T2V2
If temperature increases, volumes decreases and vice versa
⇒V2>V1 then T2<T1.
Similar Questions
For an ideal monoatomic gas, an illustration of three different paths A,(B+C) and (D+E) from an initial state P_(1),V_(1),T_(1) to a final state P_(2),V_(2),T_(1) is shown in the given figure . Path A represents a reversible isothermal from P_(1)V_(1)" to "P_(2),V_(2) , path (B+C) represent a reversible adiabatic expansion (B) from P_(1),V_(1),T_(1)" to " P_(3),V_(2),T_(2) followed by reversible heating of the gas at constant volume (C) from P_(3),V_(2),T_(2) " to " P_(2),V_(2),T_(1) . Path (D+E) represents a reversible expansion at constant pressure P_(1)(D) from P_(1),V_(1),T_(1) " to "P_(1),V_(2),T_(3) followed by a reversible cooling at constant volume V_(2)(E) form P_(1),V_(2),T_(3) " to "P_(2),V_(2),T_(1) What is DeltaS for path (A)?
View SolutionFor an ideal monoatomic gas, an illustration of three different paths A,(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure .
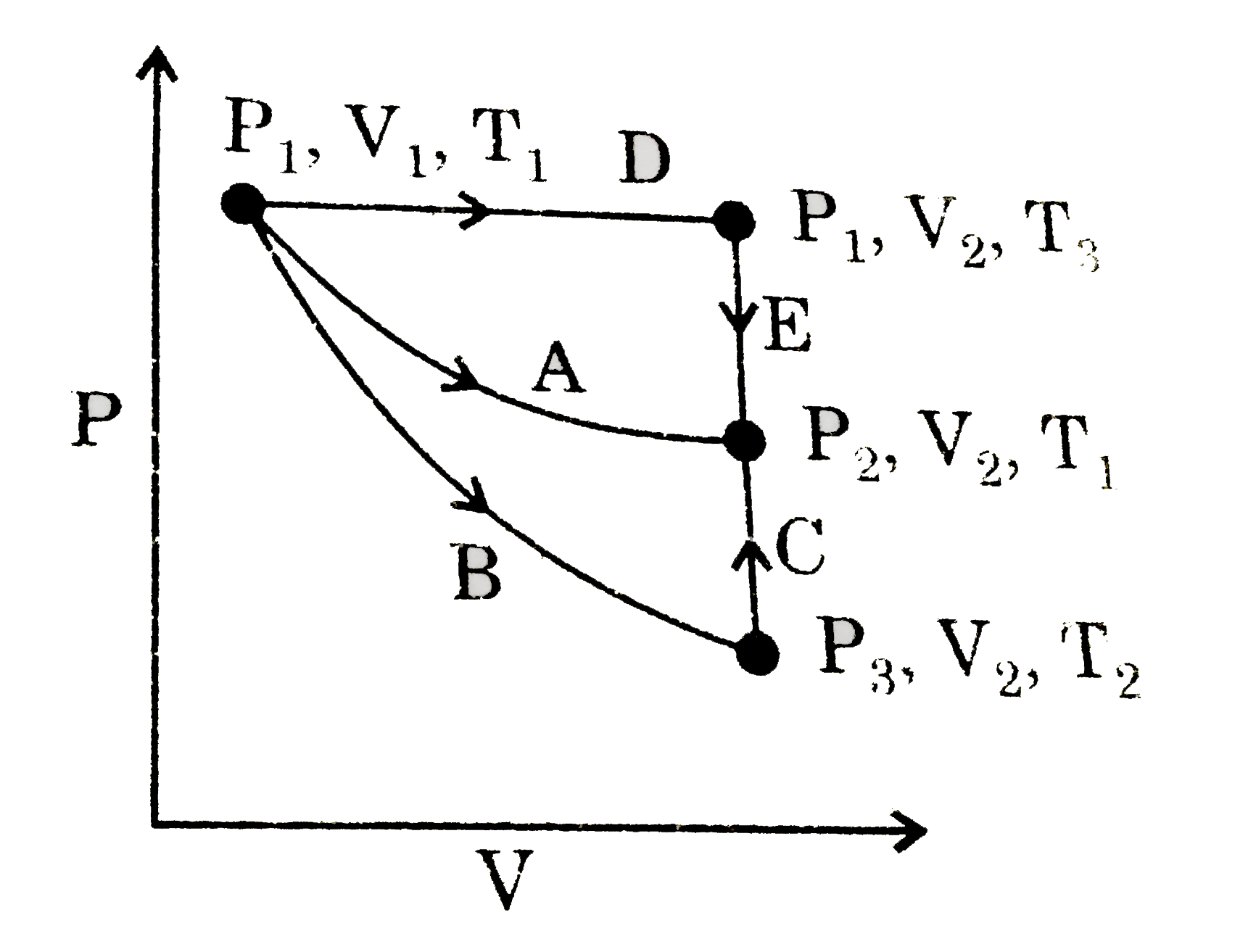
Path A represents a reversible isothermal from P1V1 to P2,V2, path (B+C) represent a reversible adiabatic expansion (B) from P1,V1,T1 to P3,V2,T2 followed by reversible heating of the gas at constant volume (C) from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) form P1,V2,T3 to P2,V2,T1
What is ΔS for (D+E)?
View SolutionEstablish gas equation, (P_(1)V_(1))/(T_(1))=(P_(2)V_(2))/(T_(2)) .
View SolutionA sample of gas changes from p1,V1 and p2. V2andT2 by one path and then back to p1,V1andT1. ΔU for the process is :
View Solutionसमतापी प्रक्रम की प्रारम्भिक स्थित (P1,V1,T1) अन्तिम स्थित (P2,V2,T2) तक परिवर्तित होती है यदि यह परिवर्तन एक मोल आदर्श गैस के लिए हो तो एट्रांपी परिवर्तन होगी
View SolutionA gas with CP/CV= goes from an initial state (P1,V1,T1) to a final state (P2,V2,T2) through an adiabatic process. The work done by the gas is
a)nR(T1−T2)γ−1
b)P1V1−P2V2γ−1
c) nRγ(T1−T2)
View SolutionA gas with C_(P)//C_(V)=gamma goes from an initial state (P_(1), V_(1), T_(1)) to a final state (P_(2), V_(2), T_(2)) through an adiabatic process. The work done by the gas is a) (nR(T_(1)-T_(2)))/(gamma-1) b) (P_(1)V_(1)-P_(2)v_(2))/(gamma-1) c) nR gamma(T_(1)-T_(2))
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P_(1), V_(1), T_(1) to a final state P_(2), V_(2),T_(1) is shown in the given figure. Path A represents a reversible isothermal expansion form P_(1),V_(1) to P_(2),V_(2) , Path (B+C) represents a reversible adiabatic expansion (B) from P_(1),V_(1),T_(1)to P_(3),V_(2),T_(2) followed by reversible heating the gas at constant volume (C) from P_(3),V_(2),T_(2) to P_(2),V_(2),T_(1) . Path (D+E) represents a reversible expansion at constant pressure P_(1)(D) from P_(1),V_(1),T_(1) to P_(1),V_(2),T_(3) followed by a reversible cooling at constant volume V_(2)(E) from P_(1),V_(2),T_(3) to P_(2),V_(2),T_(1) . What is q_(rev) , for path (A) ?
View Solution