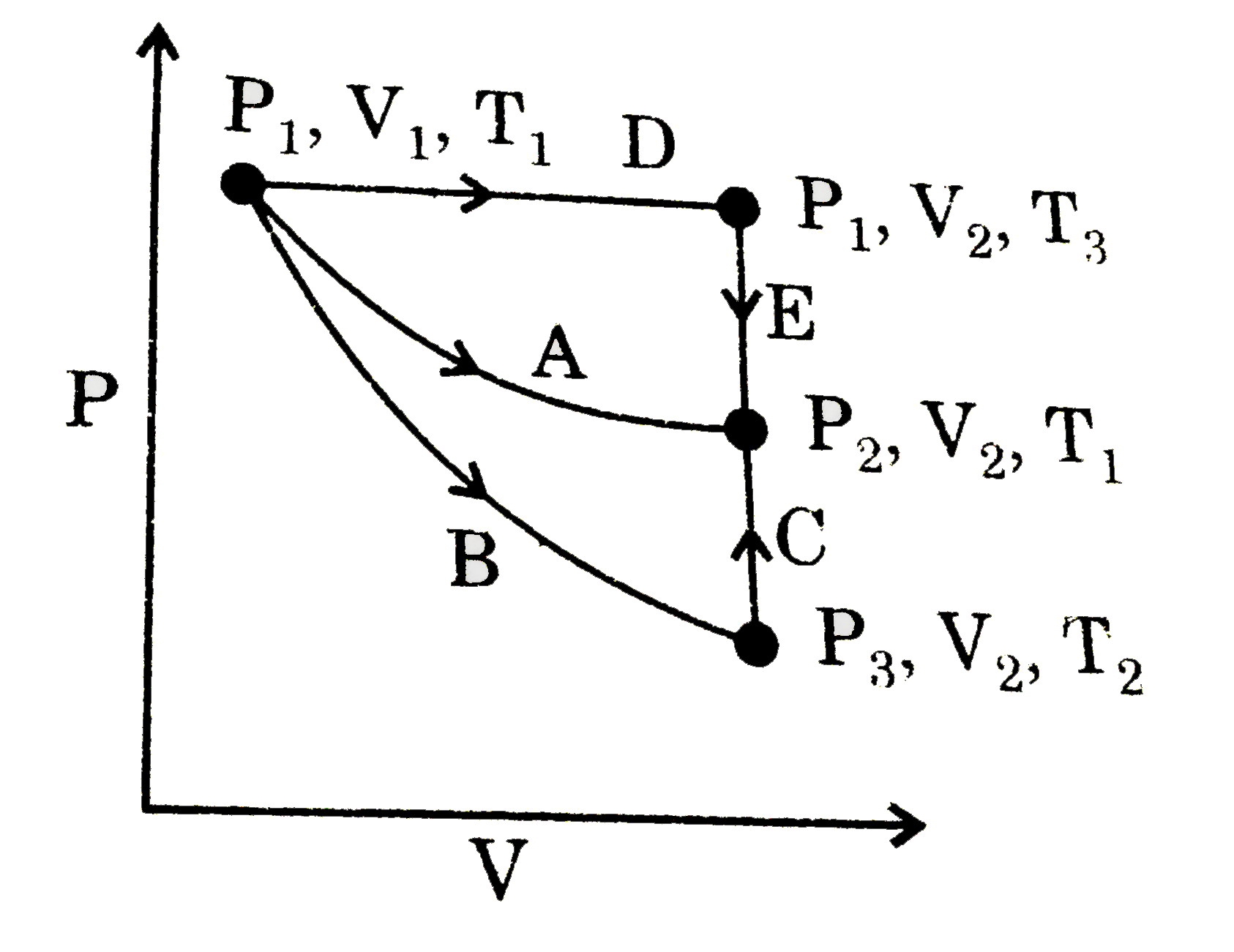
For an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
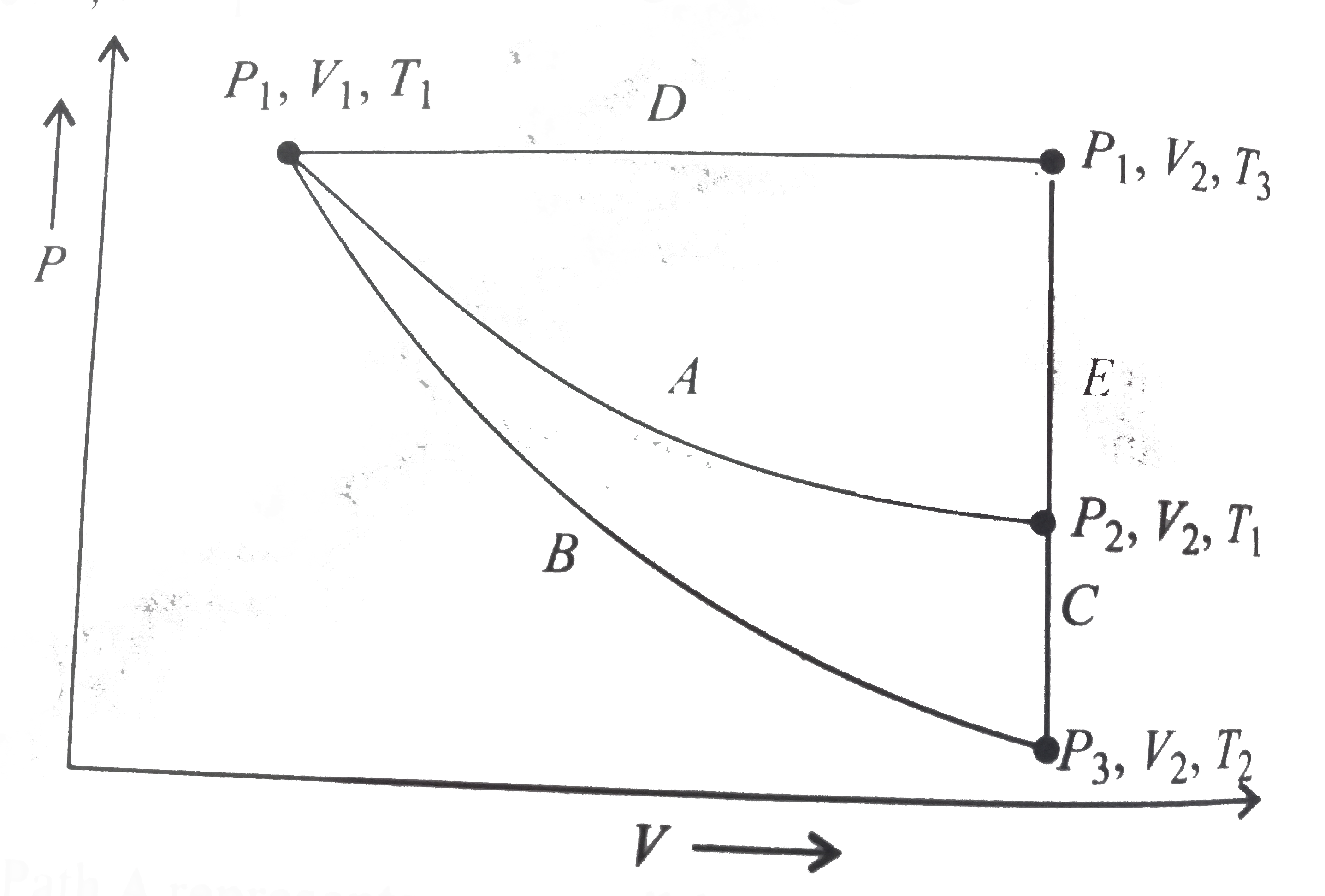
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is qrev, for path (B+C)?
nRInV2V1
−nRInV2V1
zero
nRT1InV2V1
Path (B+C) occurs in adiabatic conditions
∴Q=0
We know that
ΔS=qrevT
∴Qrev=TΔS
∴Qrev=nRInV2V1
Topper's Solved these Questions
- THERMODYNAMICSBOOK - CENGAGE CHEMISTRYCHAPTER - THERMODYNAMICSEXERCISE - Exercises (Multiple Correct)
50 Videos
- THERMODYNAMICSBOOK - CENGAGE CHEMISTRYCHAPTER - THERMODYNAMICSEXERCISE - Exercises (Single Correct)
62 Videos
- THERMODYNAMICSBOOK - CENGAGE CHEMISTRYCHAPTER - THERMODYNAMICSEXERCISE - Exercises (Subjective)
70 Videos
- STOICHIOMETRYBOOK - CENGAGE CHEMISTRYCHAPTER - STOICHIOMETRYEXERCISE - Archives Subjective
33 Videos
Similar Questions
A gas with cpcV=γ goes from an intial state (p1,V1,T1) to a final state (p2,V2,T2) through an adiabatic process. The work done by the gas is
View SolutionFor an ideal monoatomic gas, an illustration of three different paths A,(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure .
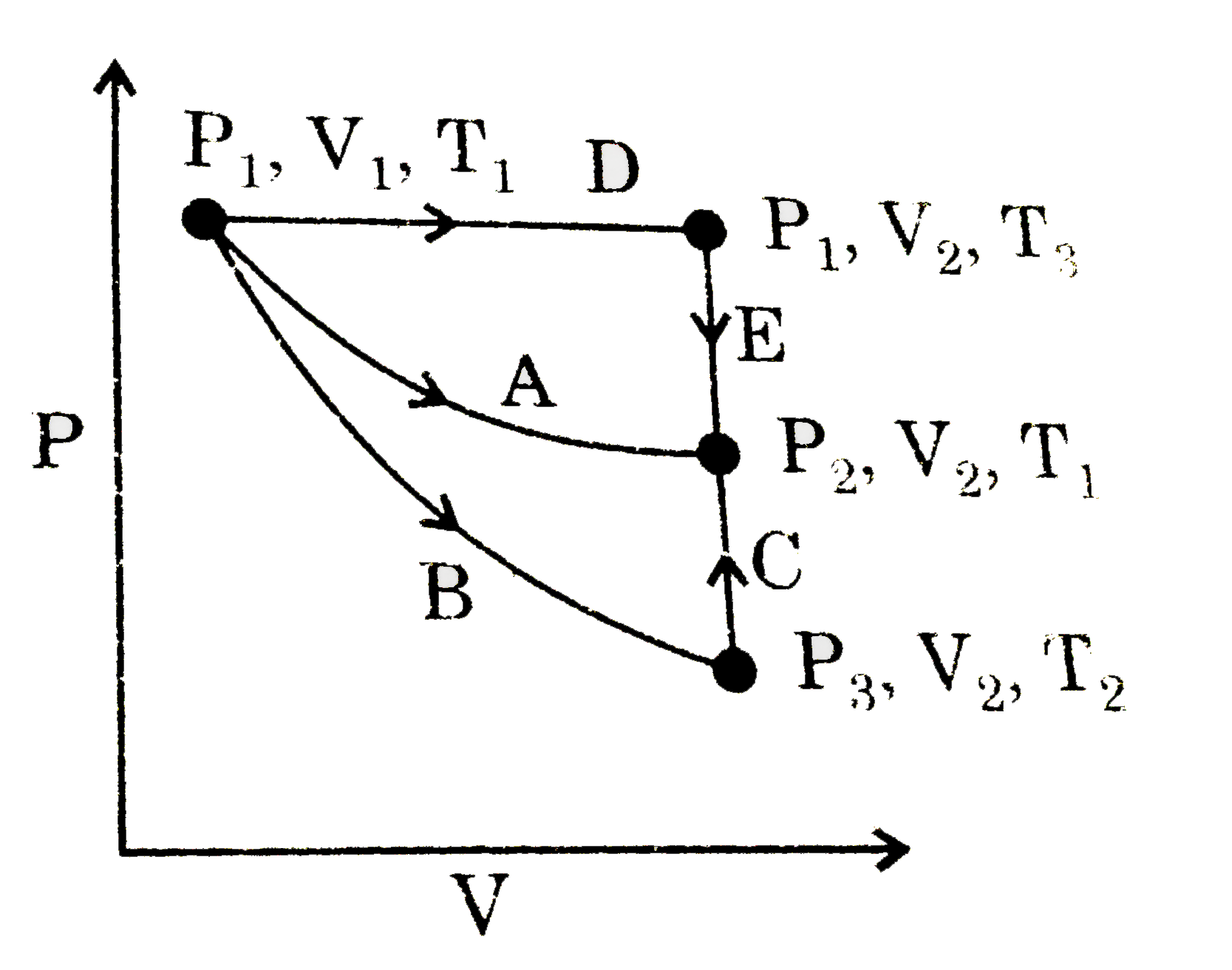
Path A represents a reversible isothermal from P1V1 to P2,V2, path (B+C) represent a reversible adiabatic expansion (B) from P1,V1,T1 to P3,V2,T2 followed by reversible heating of the gas at constant volume (C) from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) form P1,V2,T3 to P2,V2,T1
What is qrev for path (A)?
View Solution
Knowledge Check
For an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
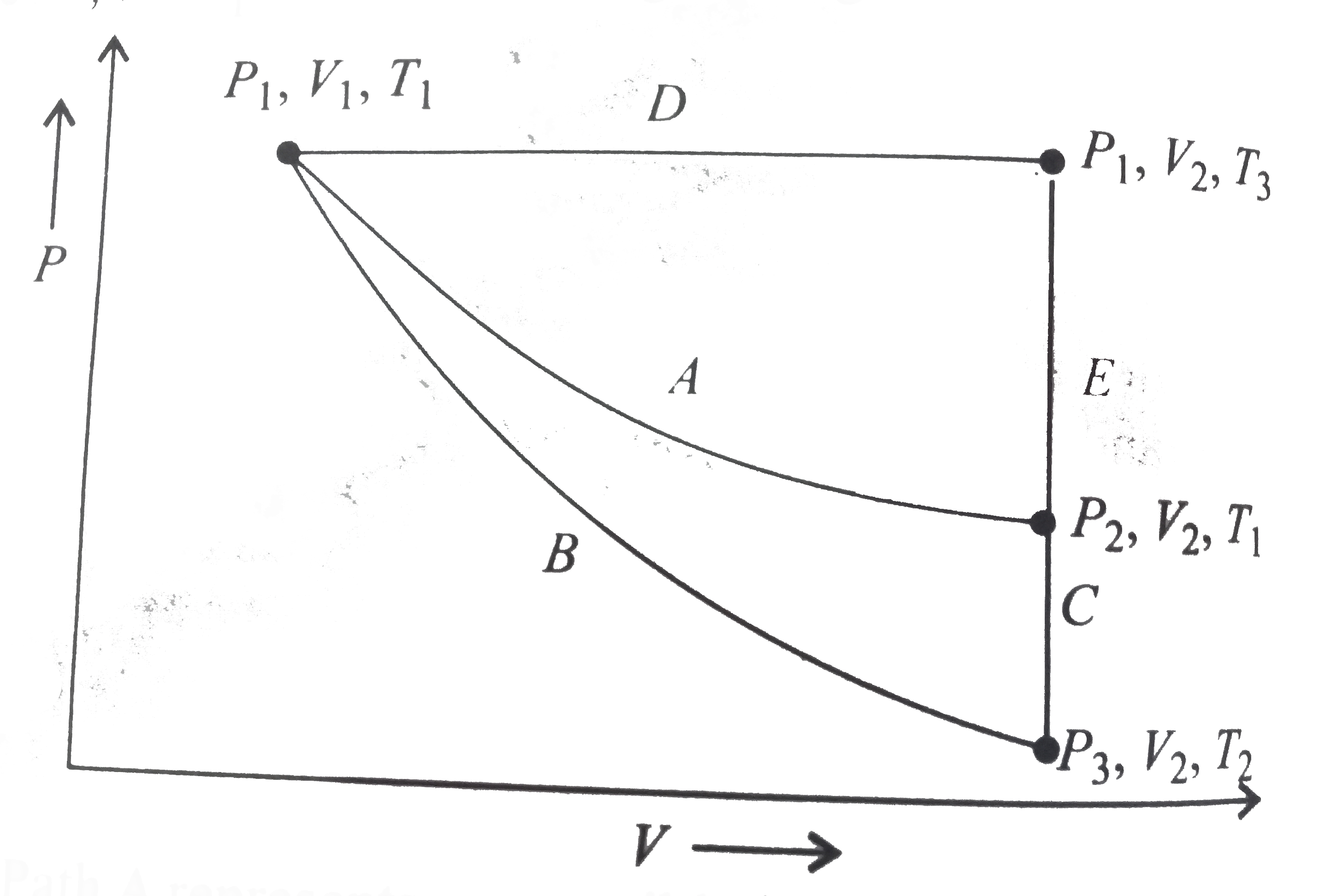
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is ΔS for path (D+E)?A−P(V2−V1)B−nRInV2V1C+P(V2−V1)DnRInV2V1For an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
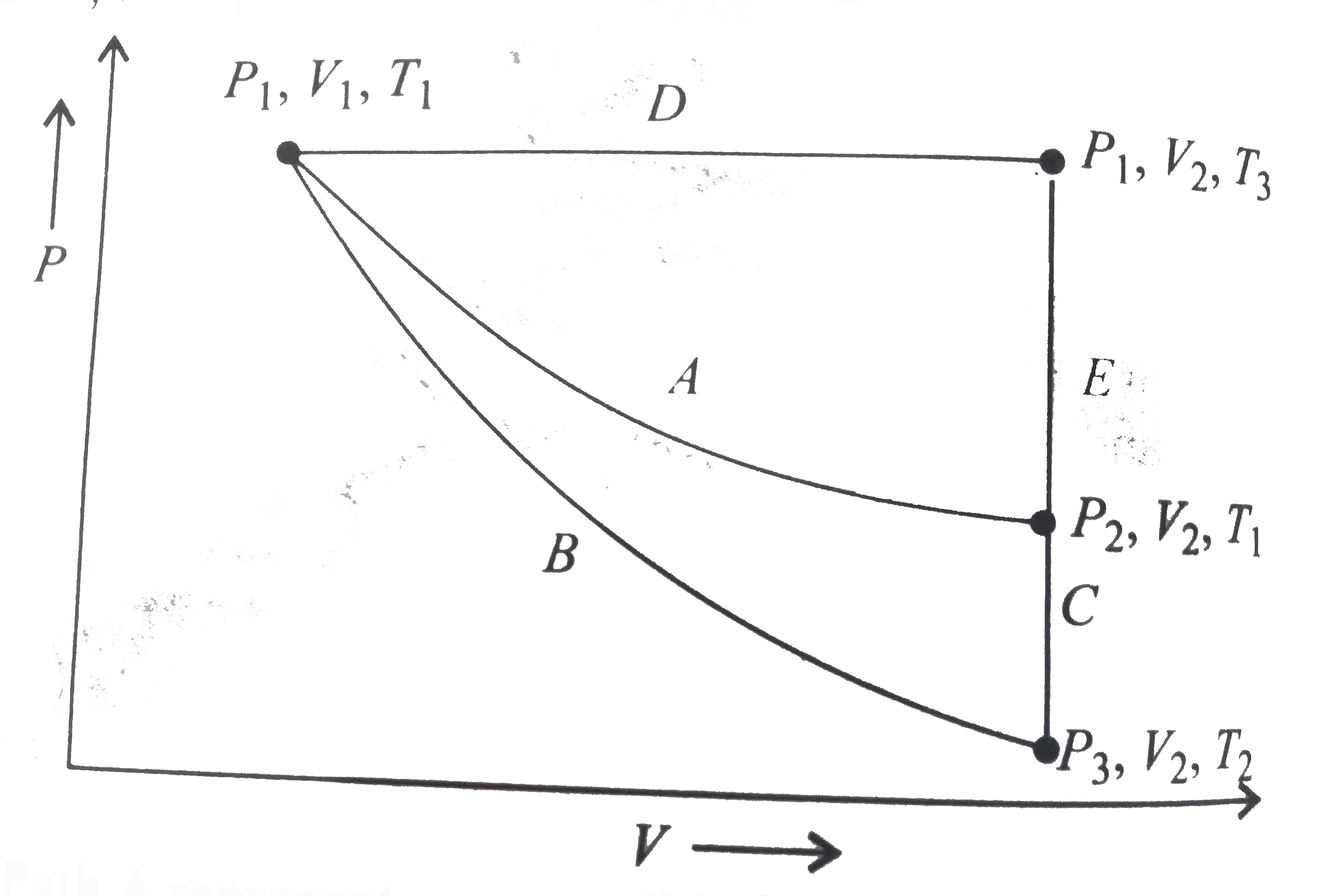
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is ΔS for path A?AnRInV2V1BP(V2−V1)C−P(V2−V1)DnR(V2−V1)For an ideal monoatomic gas, an illustration of three different paths A,(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure .
Path A represents a reversible isothermal from P1V1 to P2,V2, path (B+C) represent a reversible adiabatic expansion (B) from P1,V1,T1 to P3,V2,T2 followed by reversible heating of the gas at constant volume (C) from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) form P1,V2,T3 to P2,V2,T1
What is ΔS for path (A)?Anr InV2V1B−nr InV2V1CzeroDnR(V2−V1)
For an ideal monoatomic gas, an illustration of three different paths A,(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure .
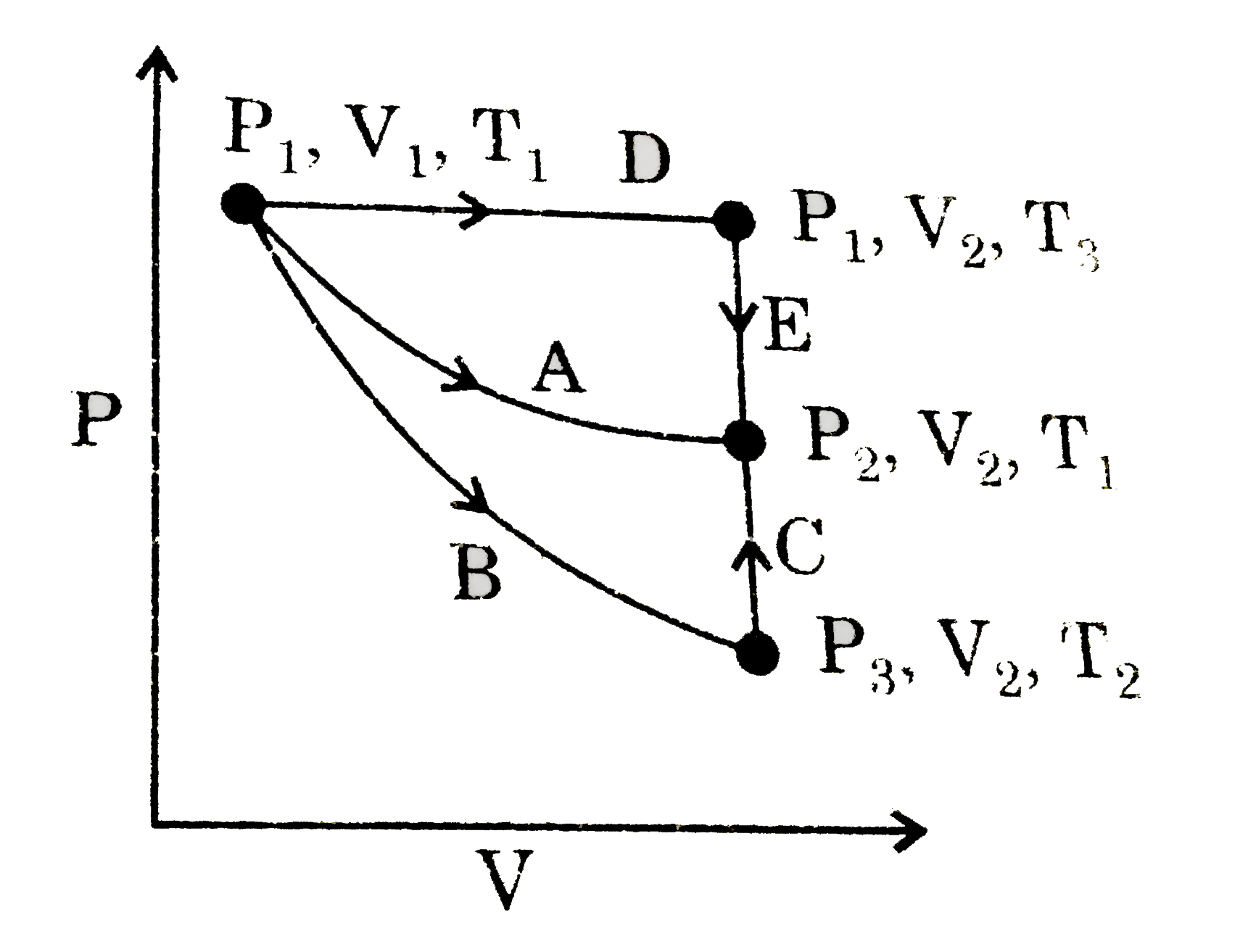
Path A represents a reversible isothermal from P1V1 to P2,V2, path (B+C) represent a reversible adiabatic expansion (B) from P1,V1,T1 to P3,V2,T2 followed by reversible heating of the gas at constant volume (C) from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) form P1,V2,T3 to P2,V2,T1
What is ΔS for (D+E)?
View SolutionFor an ideal gas, an illustration of the different paths, A (B+C) and (D+E) from an intial state P1,V1,T1 to a final state P2,V2,T1 as shown in the given figure.
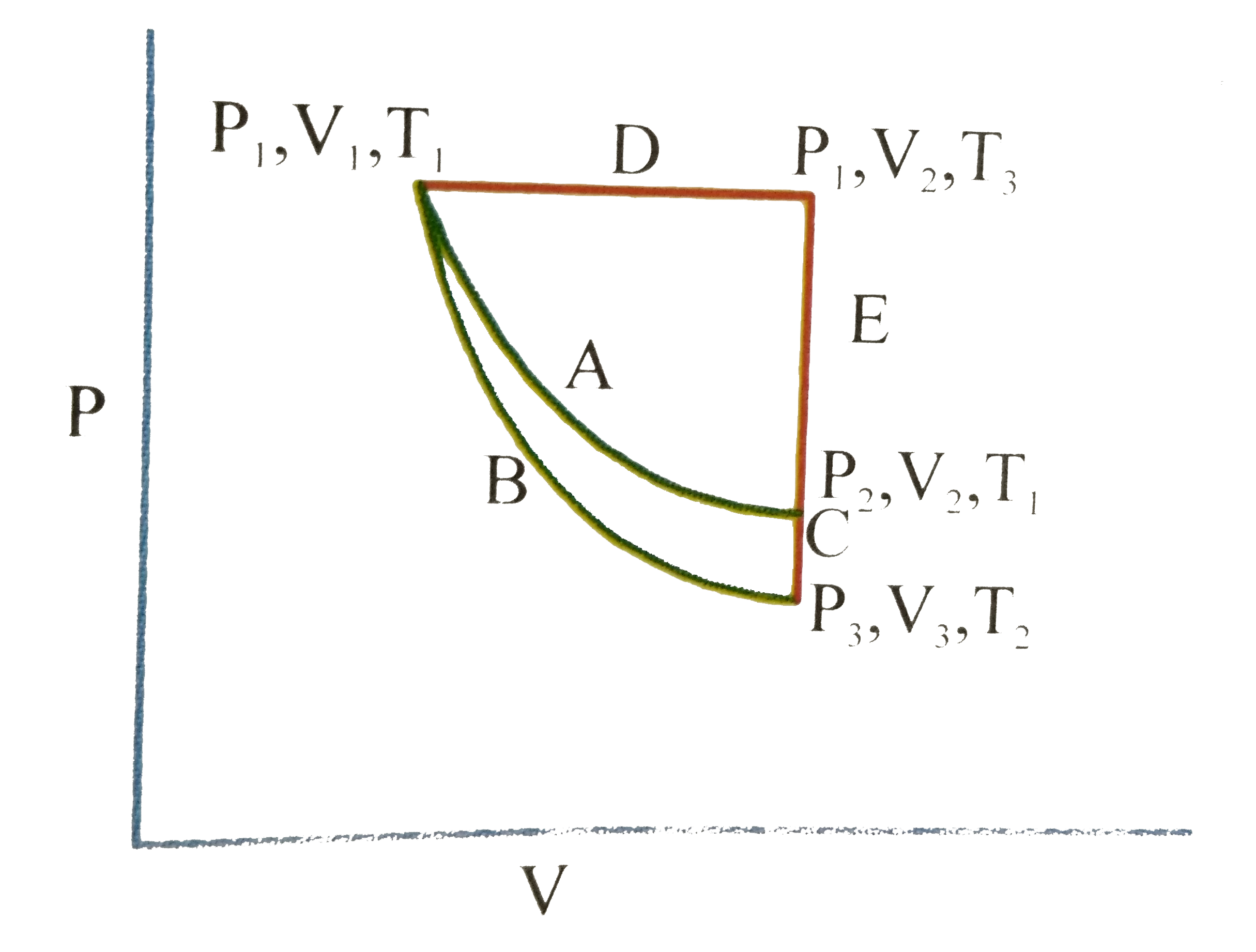
Path (A) represents a reversible isothernal expanison from P1V1 to P2V2. Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1 to P3,V2,T2 followed by reversible heating the gas at constant volume (C) from P3,V2,T2 to P2,V2T1 to P1,V2,T3 followed by reversible cooling at a constant volume V2 (E) from P1,V2,T3 to P2,V2,T1
What is ΔS for path (D+E) ?
View SolutionA system changes from the state (P1,V1) to (P2,V2) as shown in the figure below. What is the work done by the system –
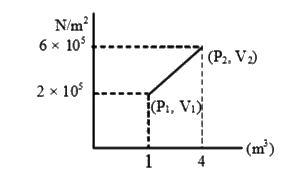
View SolutionIn an adiabatic process, the state of a gas is changed from P1,V1,T1,toP2,V2,T2. Which of the following relation is correct
View SolutionP1V1T1=P2V2T2 is -
View Solution
