Two rods A and B of identical dimensions are at temperature 30∘C. If A is heated upto 180∘C and B T∘C, then new lengths are the same . If the ratio of the coefficients of linear expansion of A and B is 4:3,then the value of T is
270∘C
200∘C
230∘C
250∘C
The correct Answer is:C
Changing in length in both rods are same
Δl=αlΔθ
∴α1l1Δθ1=α2l2Δθ2
4×(180−30)=(T−30)3
T=230
Similar Questions
The coefficient of linear expansion of a rod of length 1 m, at 27∘C, is varying with temperature as α = 2/T unit (300K≤T≤600K), where T is the temperature of rod in Kelvin. The increment in the length of rod if its temperature increases from 27∘C to 327∘C is
View SolutionTwo rods A and B of identical dimensions are at temperature 30∘C. If A is heated upto 180∘C and B T∘C, then new lengths are the same . If the ratio of the coefficients of linear expansion of A and B is 4:3,then the value of T is
View SolutionThe ratio of the lengths of two rods is 4 : 3. The ratio of their coefficients of cubical expansion is 2 : 3. Then the ratio of their linear expansions when they are heated through same temperature difference is
View SolutionThe ratio of the length of two rods is 4:3. The ratio of their coefficients of cubical expansion is 2:3. Then the ratio of their linear expansions when they are heated through same temperature difference is
View SolutionThe variation of length of two metal rods A and B with change in temperature are shown in fig. The coefficients of linear expansion αA for the metal A and the temperature T will be (Given αa=9×10−6/°C )
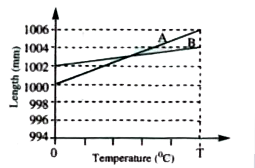
View SolutionThe ratio of the lengths of two rods is 4:3. The ratio of their coefficients of cubical expansion is 2:3. Then the ratio of their linear expansions when they are heated tnrough same temperature difference is
View SolutionTwo metal rods has lengths in the ratio 3:2 and coefficient of linear expansion are in the ratio 2:3 . If they are heated from 35^@ C to 95^@C , then ratio of their linear expansion is
View Solution
The variation of length of two metal rods A and B with change in temperature is shown in Fig. the coefficient of linear expansion αA for the metal A and the temperature T will be
View Solution
