In the figure, an ideal liquid flows through the tube, which is of uniform cross section. The liquid has velocities vA and vB, and pressures PA and PB at the points A and B, respectively. Then
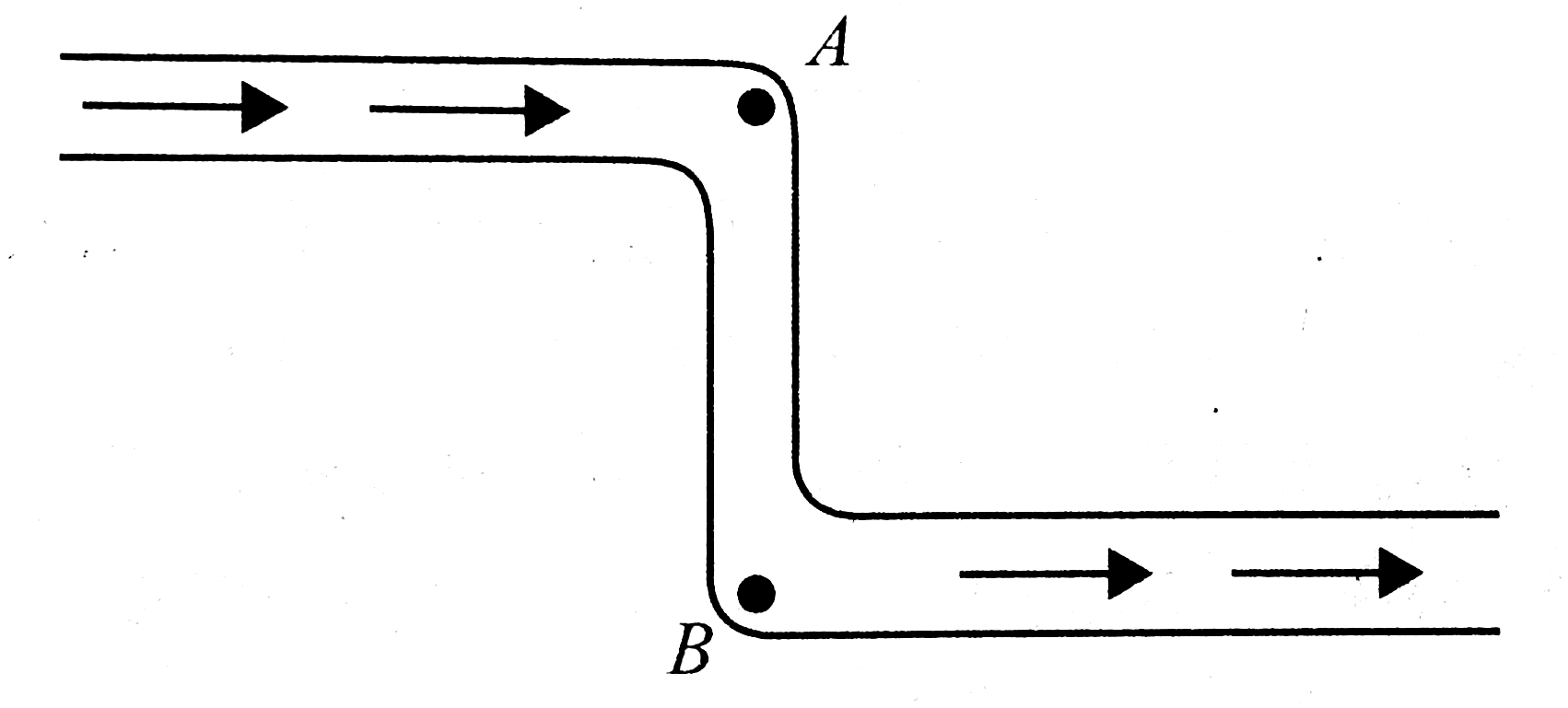
vA=vB
vB>vA
PA=PB
PB>PA
The correct Answer is:A, D
Since, area does not change hence
vA=vB
Pressure differ PB=PA+ρg(AB).
Similar Questions
In the figure, an ideal liquid flows through the tube, which is of uniform cross - section. The liquid has velocities upsilon_(A) and upsilon_(B) , and pressures p_(A) and p_(B) at points A and b respectively a) upsilon_(A)=upsilon_(B) b) upsilon_(B)gtupsilon_(A) c) p_(A)=p_(B) d) p_(B)gtp_(A)
View SolutionWater is flowing through a long horizontal tube. Let PAandPB be the pressure at two points A and B of the tube.
View SolutionIn the figure an ideal liquid flows through the tube, which is of uniform cross section. The liquid has velocities v_(A) and v_(B) and pressures p_(A) and p_(B) at points A and B respectively. a. v_(A)=v_(B) b. v_(B)gtv_(A) c. p_(A)=p_(B) d. p_(B)gtp_(A)
View SolutionWater is flowing through a long horizontal tube. Let PA and PB be the pressure at two points A and B of the tube.
View SolutionIn the figure, an ideal liquid flows through the tube, which is of uniform cross section. The liquid has velocities v_(A) and v_(B) , and pressures P_(A) and P_(B) at the points A and B , respectively. Then
View SolutionA liquid flows through a horizontal tube as shown in figure. The velocities of the liquid in the two sections, which have areas of cross-section A1 and A2 and v1 and v2 respectively. The differnece in the levels of the liquid in the two vertical tubes is h. then

View Solutionचित्र में एक आदर्श द्रव नली में बह रहा है जिसका अनुप्रस्थ परिच्छेद का क्षेत्रफल एकसमान है। द्रव का बिंदुओं क्रमश: A एवं B पर वेग v_(A) "एवं" v_(B)" तथा दाब "P_(A) "एंव" P_(B) है तो

View SolutionThe figure shown a pipe of uniform cross-section inclined in a vertical plane. A U-tube manometer is connected between the point A and B. If the liquid of density rho_(0) flows with velocity v_(0) in the pipe. Then the reading h of the manometer is
View Solution