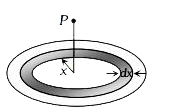
A thin uniform disc (see figure) of mass M has outer radius 4R and inner radius 3R. The work required to take a unit mass for point P on its axis to infinity is

2GM7R(4√2−5)
−2GM7R(4√2−5)
GM4R
2GM5R(√2−1)
The correct Answer is:A
Area =2πxdx
dm=M×2πxdxπ((4R)2)−π(3R)2
=2M7R2xdx
Potential dVp=−Gdm√(4R)2+x2=−G√16R2+x2×2M7R2xdx
dVp=−2GM7R2=πdx√16R2+x2
Put 16R2+x2=t2⇒2xdx=2tdt
x=3R,t=5R
x=4R,t=4√2R
Vp=2GM7R2∫4√2R5Rtdt
⇒Vp=−2GM7R2[t]4√2R5R
Vp=−2GM7R2[4√2R−5R]
W=(V∞−Vp)=0−[−2GM7R2(4√2R−5R)]
W=2GM7R2[4√2R−5R]
Similar Questions
Find the inertial moment of the disc which is punched in the middle, at its bottom and (i) the inner circle (ii) the tangent axis of the outer circle. Swatch mass M, internal radius R_(1) And outer radius R_(2) is.
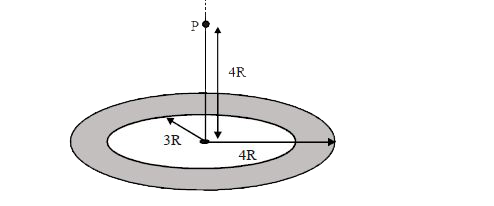
View Solutionएक पतली समरूप चकती का द्रव्यमान M, बाहरी त्रिज्या 4R एवं भीतरी त्रिज्या 3R है। एक इकाई द्रव्यमान को अक्ष पर स्थित बिन्दु P से अनन्त तक ले जाने के लिये कितने कार्य की आवश्यकता होगी।
View SolutionThe moment of inertia of hollow sphere (mass M) of inner radius R and outer radius 2R, having material of uniform density, about a diametric axis is
View SolutionA uniform metal sphere of radius R and mass m is surrounded by a thin uniform spherical shell of same mass and radius 4R. The centre of the shell C falls on the surface of the inner sphere. Find the gravitational fields at points A and B.

View SolutionA thin uniform disc (see figure) of mass M has outer radius 4R and inner radius 3R. The work required to take a unit mass for point P on its axis to infinity is
View Solutionजैसा कि चित्र में दिखाया गया है द्रव्यमान M की एक पतली एकसमान वलयाकार चकती की बाहरी त्रिज्या 4R और आंतरिक त्रिज्या 3R है। एक इकाई द्रव्यमान को इसकी अक्ष पर स्थित बिंदु P से अनंत तक ले जाने के लिए आवश्यक कार्य क्या है?
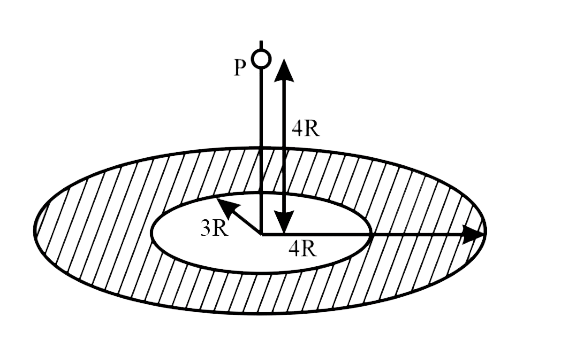
View SolutionA thin uniform disc (see figure) of mass M has outer radius 4R and inner radius 3R. The work required to take a unit mass for point P on its axis to infinity is
View SolutionA thick shell with inner radius R and outer radius 3R has a uniform charge density sigma c//m^(3) . It has a spherical cavity of radius R as shown in the figure. The electric field at the centre of the cavity is
View Solution

