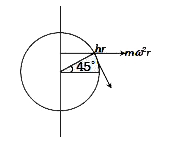
A plank is resting on a horizontal ground in the northern hemisphere of the Earth at a 45∘ latitude. Let the angular speed of the Earth be ω and its radius re. The magnitude of the frictional force on the plank will be
mreω2
mreω2√2
mreω22
Zero
The correct Answer is:C
Frmω2Rcos45∘
where re=Rcos45∘
Fr=mω2re2
Similar Questions
A body of mass m is placed at a latitude of 45^@ on earth of radius R and angular speed omega . How does the weight of the body change if earth stops rotating about its axis?
View SolutionIf .R. is the radius of the earth and .w. is angular velocity with which it rotates about its axis, the variation in the value of .g. at 45° latitude of the earth stops its rotation will be
View SolutionIf 'R' is the radius of the earth and 'w' is angular velocity with which it rotates about its axis, the variation in the value of 'g' at 45^(@) latitude of the earth stops its rotation will be
View SolutionIf 'R' is the radius of the earth and 'w' is angular velocity with which it rotates about its axis, the variation in the value of 'g' at 45∘ latitude of the earth stops its rotation will be
View SolutionBlock A of mass m rests on the plank B of mass 3m which is free to slide on a frictionless horizontal surface. The coefficient of friction between the block and plank is 0.2. If a horizontal force of magnitude 2 mg is applied to the plank B, the acceleration of A relative to the plank and relative to the ground respectively, are :
View SolutionThe diagram shows a rough plank resting on a cylinder with one and of the plank on rough ground. Negtect friction between plank and cylinder. Draw digrams to show (a) the force acting on the plank, (b)the force acting on the cylinder.
View SolutionA uniform disc of mass M and radius R initially stands vertically on the right end of a horizontal plank of mass M and length L, as shown,
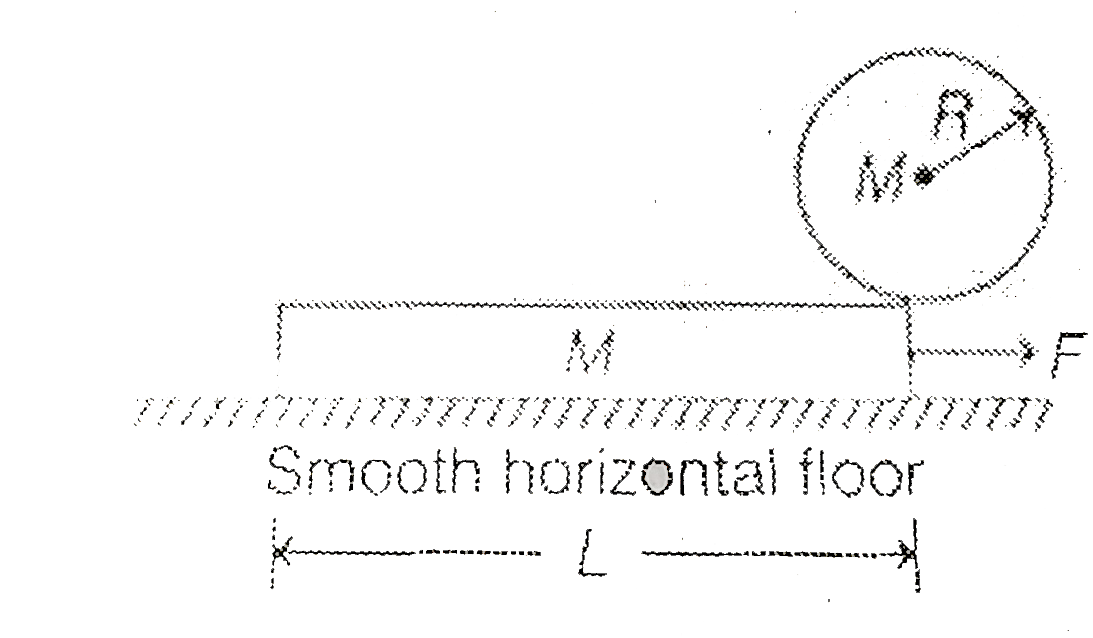
The plank rests on a smooth horizontal floor and friction between disc and plank is sufficiently high such that disc rolls on plank without slipping . The plank is pulled to right with a constant horizontal force of magnitude F.
The magnitude of acceleration of plank is
F/ 6 M
F/ 4 M
3 F/ 2 M
3 F/ 4 M
View SolutionA uniform disc of mass M and radius R initially stands vertically on the right end of a horizontal plank of mass M and length L, as shown,

The plank rests on a smooth horizontal floor and friction between disc and plank is sufficiently high such that disc rolls on plank without slipping . The plank is pulled to right with a constant horizontal force of magnitude F.
The magnitude of angular acceleration of the disc is
View Solution