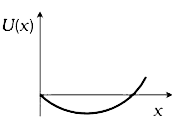
A particle which is constant to move along the x−aξs , is subjected to a force in the same direction which varies with the distance x of the particle from the origin as F(x)=−Kx+ax3 . Hero K and a are positive constant . For x≥0, the fanctional from of the patential every U(x) of the particle is


The correct Answer is:D
F(x)=−kx+ax3
U(x)=−∫F(x)dx=−∫(−kx+ax3)dx
=−−kx22+ax44⎤⎥⎦=−x2[−k2+ax24]
U= 0 at x= 0, x=√2ka
For x>√2ka,U→ (-ve)
At x= 0, F=0
Slope of U-x graph is zero, at x= 0
Similar Questions
एक कण मूल बिन्दु पर स्थित है और एक बल F=kx कण पर कार्यरत है (जहाँ, k एक धनात्मक नियतांक है।) यदि U(0)=0 हो, तो U(x) व X क मध्य आरेख होगा (जहाँ U फलन की ष्टिटीज ऊर्जा है)।
View SolutionA particle, which is constrained to move along the x-axis, is subjected to a force in the same direction which varies with the distance of the particle from the origin as F(x) =-kx+ax^(3) . Hence k and a are positive constants. For 20. the functional form of the potential energy U(x) of the particle is:
View SolutionA particle which is constrained to move along x - axis, is subjected to a force in the same direction which varies with the distance x of the particle from the origin as F(x)=kx+ax3. Here, k and a are positive constants. For x≥0, the functional form of the potential energy U (x) of the particle is
View SolutionA particle which is constant to move along the x−aξs , is subjected to a force in the same direction which varies with the distance x of the particle from the origin as F(x)=−Kx+ax3 . Hero K and a are positive constant . For x≥0, the fanctional from of the patential every U(x) of the particle is
View Solutionएक कण जो x अक्ष के अनुदिश गति कर सकता है पर एक बल जो समान दिशा में आरोपित है तथा मूल बिंदु से कण कि दुरी x के साथ F(x)=−kx+ax2 का फलन है । यहाँ k व a धनात्मक नियतांक है । x≥0 के लिए कण कि स्थितिज ऊर्जा का रेखाचित्र होगा-
View SolutionA particle, which is constrained to move along x-axis, is subjected to a force in the some direction which varies with the distance x of the particle from the origin an F (x) =-kx + ax^(3) . Here, k and a are positive constants. For x(ge0, the functional form of the potential energy (u) U of the U (x) the particle is. (a) , (b) , (c) , (d) .
View SolutionA force F=−Kx2(x≠0) acts on a particle along the X - axis. Find the work done by the force in displacing the particle from x + a to x = + 2 a . Take K as a positive constant .
View Solutiona particle is moving under the influence of a force given by F= kx , where k is a constant and x is the distance moved the energy (in joules ) gained by the particle in moving from x=0 to x=3 is
View Solution
