A particle which is constant to move along the x−aξs , is subjected to a force in the same direction which varies with the distance x of the particle from the origin as F(x)=−Kx+ax3 . Hero K and a are positive constant . For x≥0, the fanctional from of the patential every U(x) of the particle is




The correct Answer is:D
F=−dUdx⇒dU=−Fdx
⇒U=−∫x0(−Kx+ax3)dx=kx22−ax44
∴ We get U = 0 at x = 0 and x=√2K/a
and also U = negative for x>√2k/a.
So F = 0 at x = 0
i.e. slope of U-x graph is zero at x = 0.
Topper's Solved these Questions
- BOOK - ERRORLESS CHAPTER - WORK , ENERGY , POWER AND COLLISIONEXERCISE - Assertion & Reason For AIIMS Aspirants30videos
WORK , ENERGY , POWER AND COLLISION
- BOOK - ERRORLESS CHAPTER - WORK , ENERGY , POWER AND COLLISIONEXERCISE - Self Evaluation Test19videos
WORK , ENERGY , POWER AND COLLISION
- BOOK - ERRORLESS CHAPTER - WORK , ENERGY , POWER AND COLLISIONEXERCISE - Critical Thinking (Objective Questions)20videos
WORK , ENERGY , POWER AND COLLISION
- BOOK - ERRORLESS CHAPTER - WAVES AND SOUNDEXERCISE - SET25videos
WAVES AND SOUND
- BOOK - ERRORLESS CHAPTER - WORK, ENERGY, POWER & COLLISIONEXERCISE - Assertion30videos
WORK, ENERGY, POWER & COLLISION
Similar Questions
A particle, which is constrained to move along x-axis, is subjected to a force in the some direction which varies with thedistance x of the particle from the origin an F(x)=−kx+ax3. Here, k and a are positive constants. For x(≥0, the functional form of the potential energy (u) U of the U (x) the porticle is.
(a)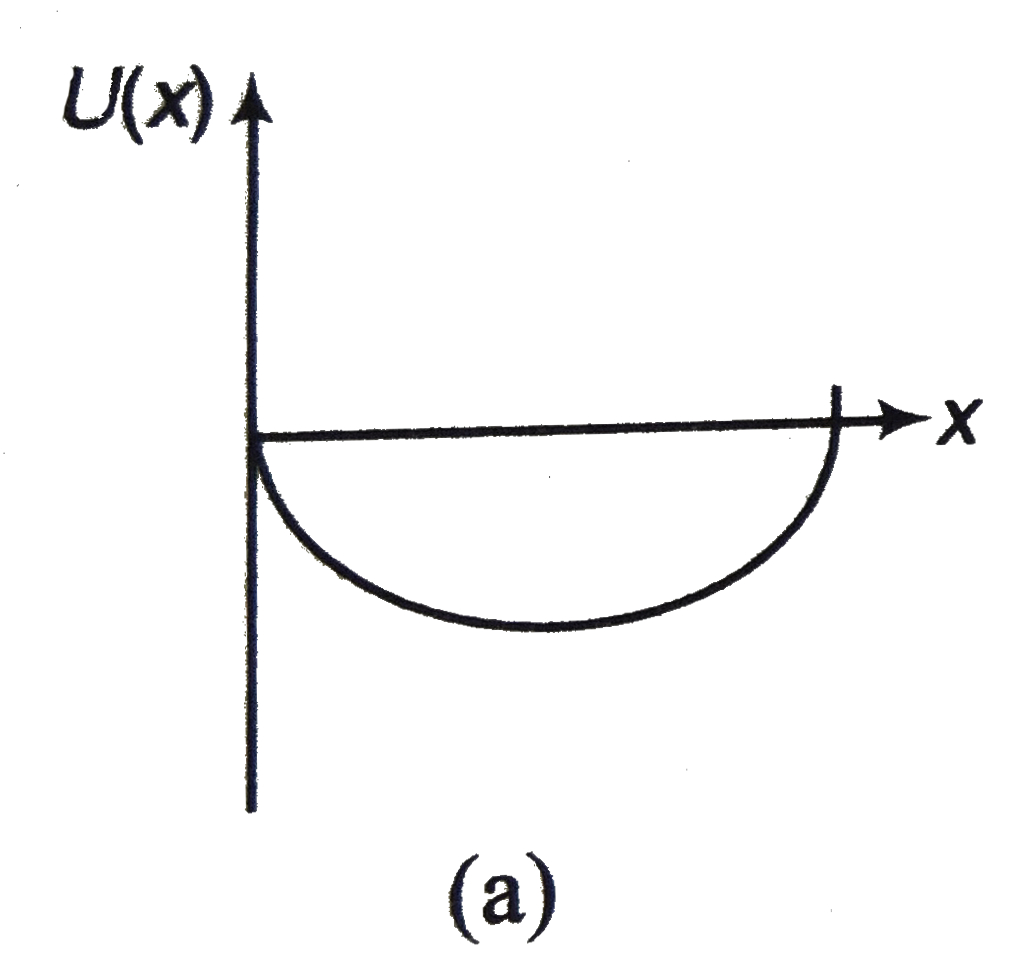 , (b)
, (b) 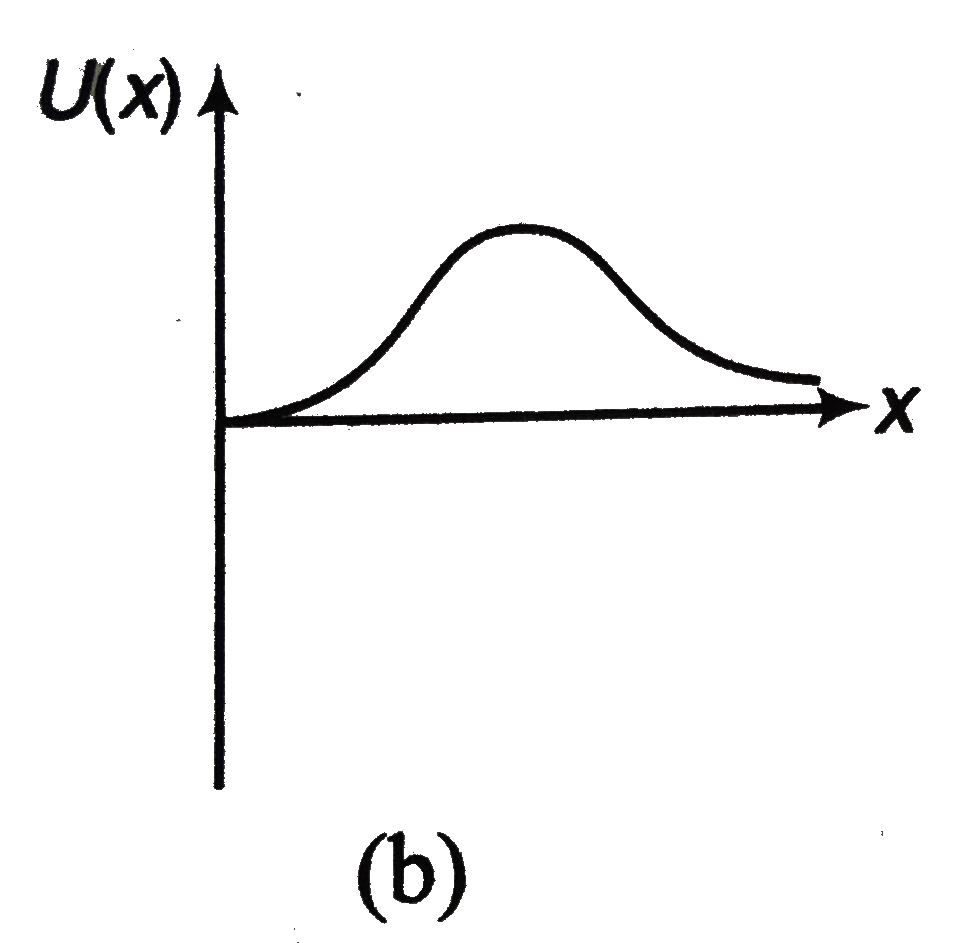 , (c)
, (c) 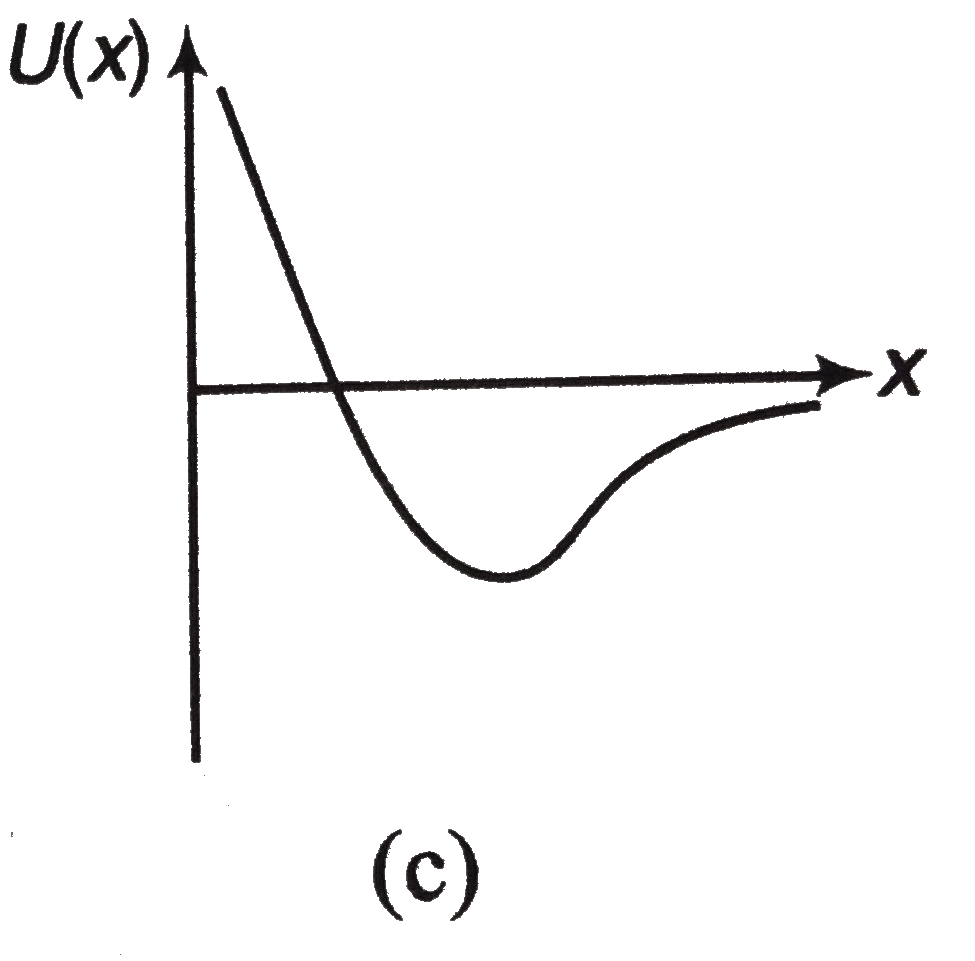 , (d)
, (d) 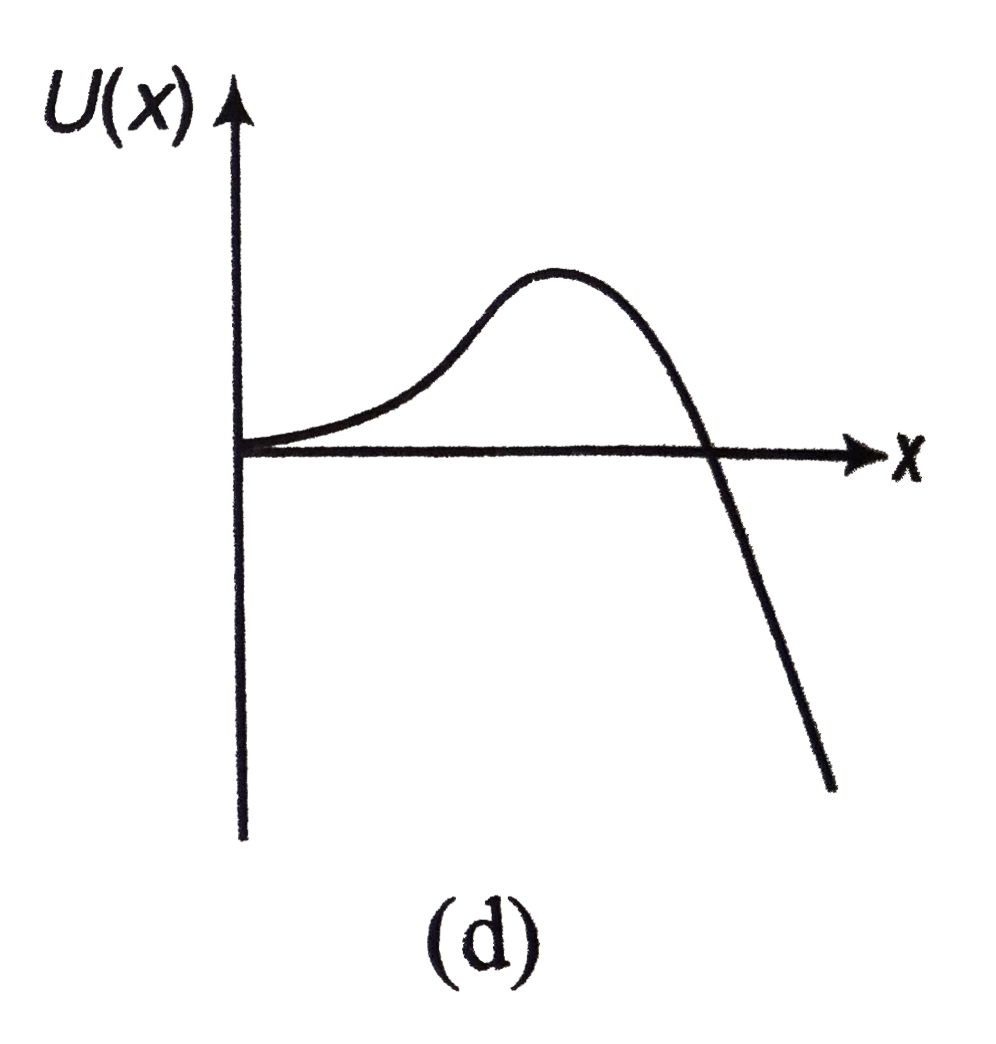 . View Solution
. View SolutionThe kinetic energy of a particle moving along x-axis varies with the distance x of the particle from origin as K=A+x3Bx1/4+C .Write the dimensional formula for A2B
View Solution
Knowledge Check
- Question 1 - Select One
A particle which is constant to move along the x−aξs , is subjected to a force in the same direction which varies with the distance x of the particle from the origin as F(x)=−Kx+ax3 . Hero K and a are positive constant . For x≥0, the fanctional from of the patential every U(x) of the particle is
A B
B C
C D
D
- Question 2 - Select One
A particle, which is constrained to move along the x-axis, is subjected to a force from the origin as F(x)=−kx+ax3. Here k and a are origin as F(x)=−kx+ax3. Here k and a are positive constants. For x=0, the functional form of the potential energy U(x) of particle is.
A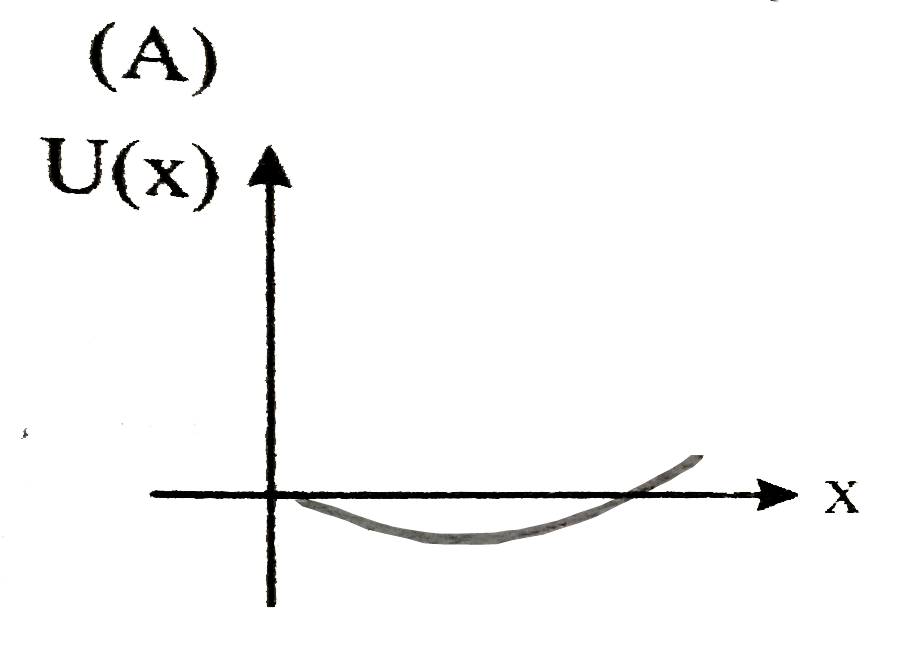 B
B C
C D
D
- Question 3 - Select One
A particle which is constant to move along the x−aξs , is subjected to a force in the same direction which varies with the distance x of the particle from the origin as F(x)=−Kx+ax3 . Hero K and a are positive constant . For x≥0, the fanctional from of the patential every U(x) of the particle is
A B
B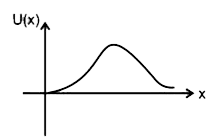 C
C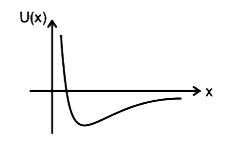 D
D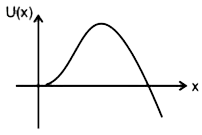
A particle moving along the x- axis is subjected to a force given by F=F0(ex/a−1) where F0 and are constants Determine an expression for the work done by this force as the particle moves from the origin to the point x=r
View SolutionA particle constrained to move along the x-axis in a
potential V=kx2 is subjected to an external time dependent
force →f(t) here k is a constant, x the distance from the origin,
and t the time. At some time T, when the particle
has zero velocity at x = 0, the external force is removed.
Choose the incorrect options –
(1) Particle executes SHM
(2) Particle moves along +x direction
(3) Particle moves along – x direction
(4) Particle remains at restView SolutionA force F=−kx2(x≠0) acts on a particle in x-direction. Find the work done by this force in displacing the particle from. x=+a to x=2a. Here, k is a positive constant.
View SolutionA particle is projected with velocity V0along axis x . The deceleration on the particle is proportional to the square of the distance from the origin i.e., a=ωx2.distance at which the particle stops is
View SolutionA particle free to move along x-axis is acted upon by a force F=−ax+bx2whrteaandbarepositiveconstants.For ximplies0, the correct variation of potential energy function U(x) is best represented by.
View Solution

