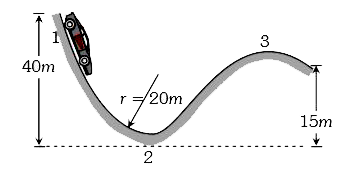
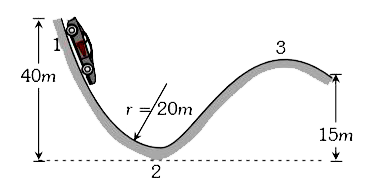
A 200kg car starts from rest at a point 1 and moves without friction down the track as shown in the figure. Determine the minimum safe value of the radius of curvature at point 3
The correct Answer is:50
By energy conservation
(T.M.E)1=(T.M.E)2⇒mgh=12mv2
v2=2gh=2×10×40
⇒v=20√2m/s (velocity at point 2)
Now, at point 2, N=mg+mv2r
=200×10+200×400×220=1000N
(T.M.E)1=(T.M.E)2⇒mgh=12mv2
v2=2gh=2×10×(40−15)=500
And mg−N=mv2R⇒mg=mv2R (as N= 0)
∴R=v2g=50010=50m
It is radius of curvature at point 3.
Similar Questions
A body of mass 'm' is moving with constant speed v on a track shown in figure. At point A and point B radius of curvature is R. NA,NB and NC represents normal reactions at A, B and C which of the following option is correct ?
View SolutionFigure shows a loop the loop track of radius R. A car (without engine) starts from a platform at a distance h above the top of the loop and goes around the loop without falling off the track. Find the minimum value of h for a successful looping. Neglect friction.

View SolutionA point particle of mass m, moves long the uniformly rough track PQR as shown in figure. The coefficient of friction, between the particle and the rough track equals μ. The particle is released, from rest from the point P and it comes to rest at a point R. The energies, lost by the ball, over the parts, PQ and QR, of the track, are equal to each other, and no energy is lost when particle changes direction from PQ to QR.
The value of the coefficient of friction μ and the distance x (=QR), are, respectively close to:

View SolutionA small roller coaster starts at point A with a speed u on a curved track as shown in the figure The friction between the roller coaster and the track is negligible and it always remains in contact with the track. The speed of roller coaster at point D on the track will be
View SolutionA solid cylinder of mass M and radius R rolls down an inclined plane of height h without slipping. The speed of its centre when it reaches the bottom is.
View SolutionIn the figure shown, a small ball of mass 'm' can move without sliding in a fixed cylindrical track of radius R in vertical plane. It is released from the top. The resultant force on the ball at the lowest point of the track is
View SolutionA point particle of mass m, moves long the uniformly rough track PQR as shown in figure. The coefficient of friction, between the particle and the rough track equals mu . The particle is released, from rest from the point P and it comes to rest at a point R. The energies, lost by the ball, over the parts, PQ and QR, of the track, are equal to each other, and no energy is lost when particle changes direction from PQ to QR. The value of the coefficient of friction mu and the distance x (=QR) , are, respectively close to:
View SolutionFigure shows the roller coaster track. Each car will start from rest at point A and will roll with negligible friciton. It is important that there should be at least some small positive normal force exerted by the track on the car at all points, otherwise the car would leave the track. With the above fact, the minimum safe value for the radius of curvature at point B is (g=10m//s^(2) :
View Solution
