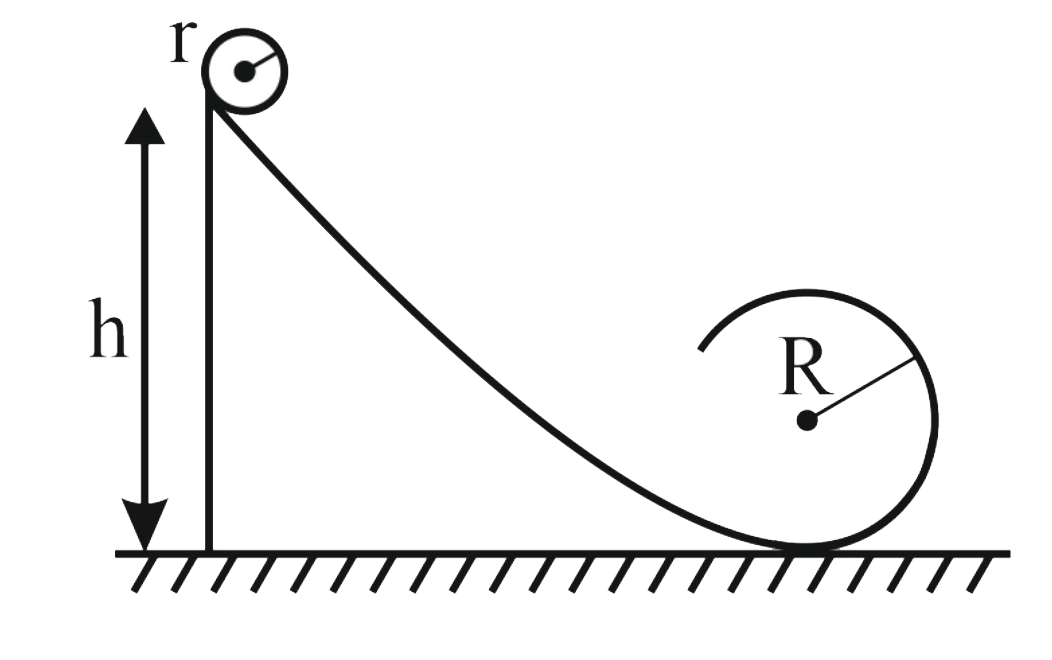
Figure shows a loop the loop track of radius R. A car (without engine) starts from a platform at a distance h above the top of the loop and goes around the loop without falling off the track. Find the minimum value of h for a successful looping. Neglect friction.

Suppose the speed of the car at the topmost point of the loop si v. Taking the gravitatioN/Al potential energy to be ero at the platform and assuming that the car starts with a negligible speed the conservation of energy shows
0=−mgh+12mv2
or, mv2=2mgh
where m is the mass of teh car. The car moving in a circle must have radial aceleration v2R at this instant. The force on the car are mg due to gravirty and N due to the contact with the tgrack. Both these forces are n radial direction at the top o the loop. Thus, from Newton's law
mg+N=mv2R
or, Mg+N=2mghR
For h to be minimum N should assume the minimum value which can be zero. Thus,
2mg(hmin)R=mgorhmin=R2
Topper's Solved these Questions
- WORK AND ENERGYBook:HC VERMA ENGLISHChapter:WORK AND ENERGYExercise:Objective -1
Explore 10 Videos
- WORK AND ENERGYBook:HC VERMA ENGLISHChapter:WORK AND ENERGYExercise:Objective -2
Explore 8 Videos
- WORK AND ENERGYBook:HC VERMA ENGLISHChapter:WORK AND ENERGYExercise:Question for Short Answer
Explore 16 Videos
- WAVE MOTION AND WAVES ON A STRINGBook:HC VERMA ENGLISHChapter:WAVE MOTION AND WAVES ON A STRINGExercise:Question for short Answer
Explore 7 Videos
Similar Questions
A solid sphere rolls without slipping along the track shown in the figure. The sphere starts from rest from a height h above the bottom of the loop of radius R which is much larger than the radius of the sphere r. The minimum value of h for the sphere to complete the loop is
View SolutionFigure shows two concentric loops of radii R and r (R gtgt r). A current i is passed through the outer loop. Find the flux linked with inner loop and the mutual inductance of the arrangement.
View SolutionA current I flows along a round circular loop of radius R. Find the line integration of magnetic field along the axis of the loop from center to ∞
View SolutionThe figure shows a circular loop of radius a with two long parallel wires (νmbered1and2) all in the plane of the paper . The distance of each wire from the centre of the loop is d. The loop and the wire are carrying the same current I. The current in the loop is in the counterclockwise direction if seen from above.
(q) The magnetic fields(B) at P due to the currents in the wires are in opposite directions.
(r) There is no magnetic field at P.
(s) The wires repel each other.
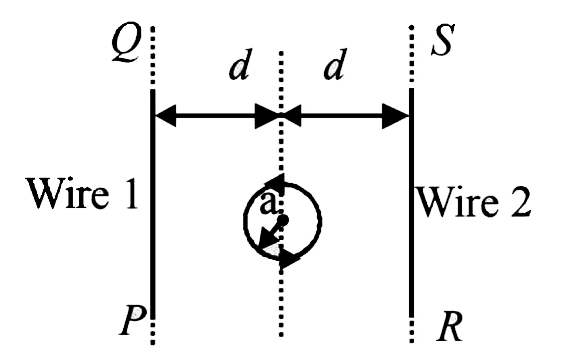
(4) When d≈a but wires are not touching the loop , it is found that the net magnetic field on the axis of the loop at a height h above the loop is zero. In that case
View SolutionThe figure shows a circular loop of radius a with two long parallel wires (νmbered1and2) all in the plane of the paper . The distance of each wire from the centre of the loop is d. The loop and the wire are carrying the same current I. The current in the loop is in the counterclockwise direction if seen from above.
.
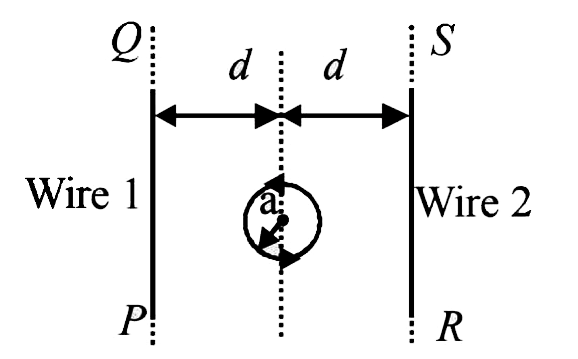
(5) Consider d>>a, and the loop is rotated about its diameter parallel to the wires by 30∘ from the position shown in the figure. If the currents in the wire are in the opposite directions, the torque on the loop at its new position will be ( assume that the net field due to the wires is constant over the loop).
View SolutionThe figure shows a circular loop of radius a with two long parallel wires (numbered 1 and 2) all in the plane of the paper . The distance of each wire from the centre of the loop is d. The loop and the wire are carrying the same current I. The current in the loop is in the counterclockwise direction if seen from above.
(q) The magnetic fields(B) at P due to the currents in the wires are in opposite directions.
(r) There is no magnetic field at P.
(s) The wires repel each other.

(4) When d≈a but wires are not touching the loop , it is found that the net magnetic field on the axis of the loop . In that case
View SolutionThe figure shows a circular loop of radius a with two long parallel wires (νmbered1and2) all in the plane of the paper . The distance of each wire from the centre of the loop is d. The loop and the wire are carrying the same current I. The current in the loop is in the counterclockwise direction if seen from above.
(q) The magnetic fields(B) at P due to the currents in the wires are in opposite directions.
(r) There is no magnetic field at P.
(s) The wires repel each other.

(5) Consider d>>a, and the loop is rotated about its diameter parallel to the wires by 30∘ from the position shown in the figure. If the currents in the wire are in the opposite directions, the torque on the loop at its new position will be ( assume that the net field due to the wires is constant over the loop).
View SolutionAn aircraft loops the loop of radius R = 500 m with a constant velocity v=360km/h. The weight of the flyer of mass m = 70 kg in the lower, upper and middle points of the loop will respectively be-
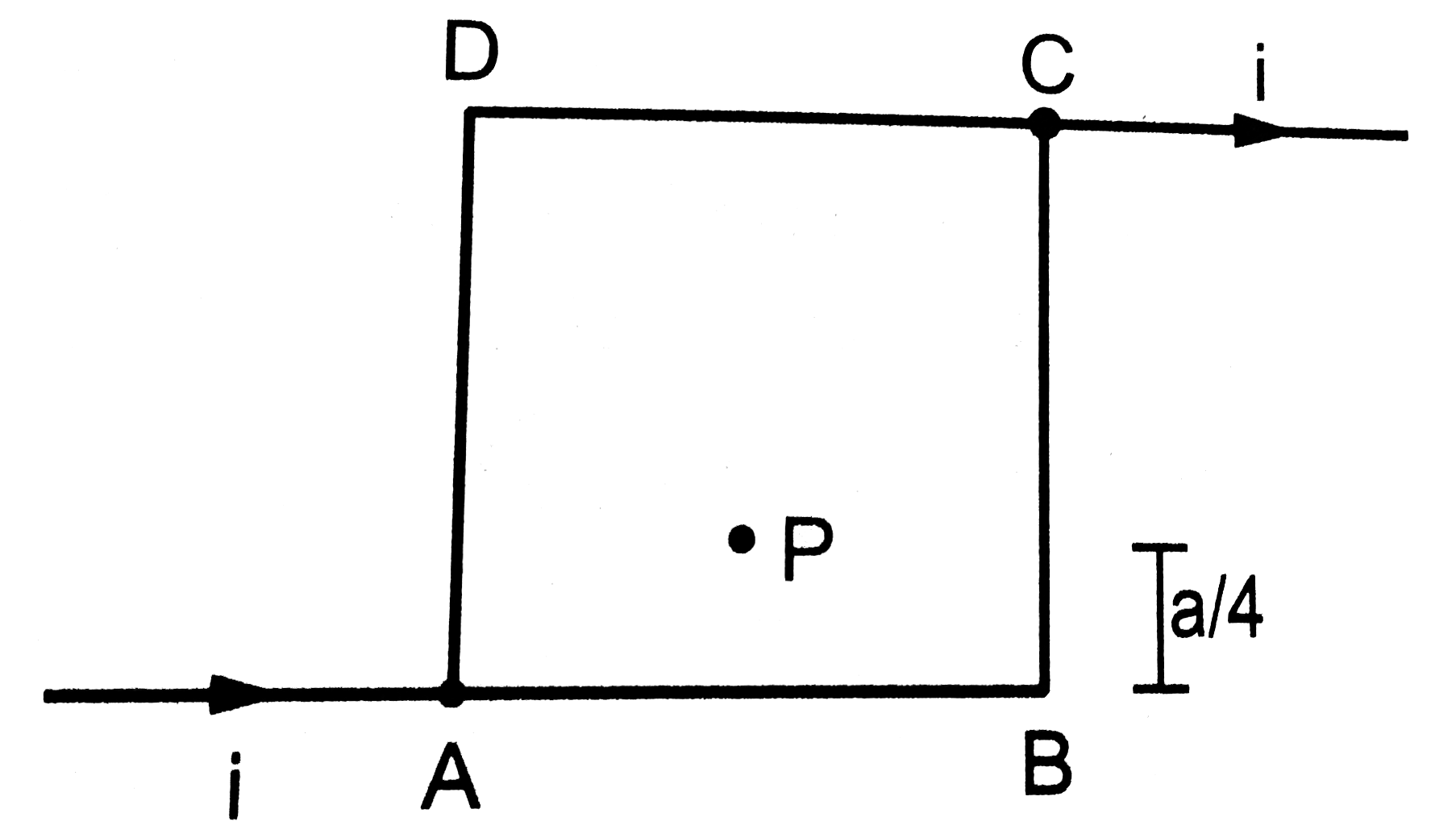
View SolutionFigure shows a square loop of edge a made of a uniform wire. A current i enters the loop at the point A and leaves it at the point C. Find the magnetic field at the point P which is on the perpendicular bisector of AB at a distance a/4 from it.
View SolutionFigure shows a long straight wire carrying current , and a square conducting wire loop of side i, at a distance 'a' from current wire. Both the current wire and loop arc in the plane of paper. Find the flux of magnetic field of current wire, passing through the loop.
View Solution

