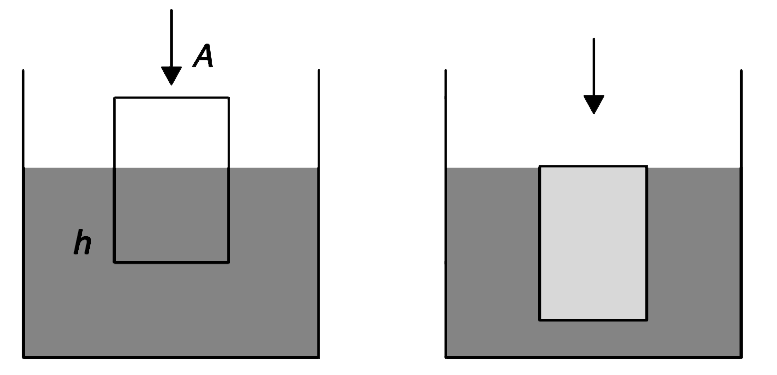
A cylindrical wooden block of density half the density of water is floating in water in a cylindrical container. The cross section of the wooden block. And its height are A and h respectively. The cross sectional area of the container is 2A. The wooden block is pushed vertically so that it gradually gets immersed in water. Calculate the amount of work done in pushing the block. Density of water =ρ0.
(h1−h2)gρ
(h1−h2)gAρ
12(h1−h2)2gAρ
14(h1−h2)2gAρ
The correct Answer is:D
h→ Common height
Conservation of mass –
ρA1h1+ρA2h2=ρh(A1+A2)
⇒h=(h1+h22) [As A1=A2=A ]
As (h12)→ initial C.G. [centre of gravity]
Similarly, (h22)→ initial C.G. [centre of gravity]
The initial potential energy
Ui=(h1Aρ)gh12+(h2Aρ)gh22=ρgA(h21+h22)2
when vessels are connected –
h2→C Centre of gravity
i.e. ((h1+h2)4) [ as h=(h1+h2)/2]
Potential energy –
Uf=[(h1+h22)Aρ]g(h1+h24)=Aρg[(h1+h2)24]
Work done by gravity –
W=Ui−Uf=14.ρgA[2h21+2h22−h21−h22−2h1h2]
W=14ρgA(h1−h2)2
Similar Questions
A wooden block of cross-sectional area 10cm2 is floating vertically on water. The volume of the immersed portion of the block is 200cm3. The block is depressed slightly inside water and then released. Calculate the time period of vibration of the block.
View SolutionA wooden block of cross sectional area 10cm2 remains floating upright in water. The volume of the immersed part of the block is 200cm3. If the block is depressed slightly and then released, determine the time period of its oscillation.
View Solutionएक लकड़ी का गुटका पारे (घनत्व 13.6 gm/cc) तथा जल (घनत्व 1gm/cc) दोनों में तैर सकता है। पारे तथा जल के विस्थापित द्रव्यमानों में अनुपात होगा
View SolutionA wooden block floats vertically in a glass filled with water . How will the level of the water in the glass change if the block is kept in a horizontal position ?
View Solutionएक लकड़ी का गुटका अपने डुबे हुए आयतन के (4/5)^("वें") भाग के साथ जल में तैरता है। यदि इसकी समान कोई गुटका किसी द्रव में तैरता है, तो उस द्रव का घनत्व "(किग्रा/मी"^(3) में) क्या है?
View SolutionA cylindrical block of wood of mass m and area cross-section A is floating in water (density = rho ) when its axis vertical. When pressed a little and the released the block starts oscillating. The period oscillations is
View SolutionA wooden block floats in water with two third of its volume submerged. A. Calculate the density of wood.b. When the same block is placed in oil, three - quarter of its volume in immersed in oil. Calculate the density of oil.
View SolutionA wooden block floats in water with two-third of its volume submerged.
When the same block is placed in oil, three quarters of its volume is immersed in oil. Calculate the density of oil.
View Solution
