Block B of mass mB=0.5kg rests on block A, with mass mA=1.5kg which in turn is on a horizontal tabletop (as shown in figure) .The coefficient of kinetic friction between block A and the tabletop is μk=0.4 and the coefficient of static friction between block A and blockB is μs=0.6 A light string attached block A passes over a frictionless, massless pulley and block C is suspended from the other end of the string. What is the largest mass mc (in kg) that block C can have so that block A and B still slide together when the system is replaced from rest?

The correct Answer is:5
Denote the common magnitude of the maximum acceleration as a. For block A to remain at rest with respect to block B,a≤μsg. Let us assume a=msg for mass of C to be largest. The tension in the cord is then
T=(mA+mB)a+μkg(mA+mB)
=(mA+mB)(a+μkg)
This tension is related to the mass mC (Largest) by
T=mC(g−a)
Solving for mC yields
mC=(mA+mB)(μs+μk)1−μs
=(1.5+0.5)(0.6+0.4)1−0.6=5kg
Similar Questions
Coefficient of kinetic friction and coefficient of static friction between two blocks is μk and μs respectively. In general
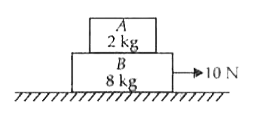
View SolutionBlock A of mass 2 kg is placed over block B of mass 8 kg .The combination is placed over a rough horizonatal surface .Cofficient of friction between B and the floor is 0.5 .Coefficient of friction berween A and B is 0.4 .A horizontal force of 10 N is applied on block B .The force of friction between A and B is
(g=10 ms−2)
View SolutionA block of mass m2 is placed on a horizontal table and another block of mass m1 is placed on top is it. An increasing horizontal force F=αt is exerted on the upper block but the lowwer block never moves as a result. If the coefficient of friction between the blocks is μ1 coefficient of friction between the blocks is μ1 and that between the lower block and the table is μ2, then what is the maximum possible value of μ1/μ2 ?
View SolutionA block A of mass m_1 rests on a horizontal table. A light string connected to it passes over a frictionless pulley at the edge of table and from its other end another block B of mass m_(2) is suspended. The coefficient of knetic friction between the block and table is mu_(k) . When the block A is sliding on the table, the tension in the string is.
View SolutionA block with mass m1 is placed on an inclined plane with slope angle α and is connected to a second hunging block with mass m2 by a cord passing over a small . Friction less pulley as shown in fig 7.247 . The coefficient of static friction is μ2 and the coefficient of kinetic friction is μs

a. Find the mass m2 for which block m1 moves up plane at constant speed once it is set in motion
b. Find the mass m2 for which block m1 moves down the plane at constant speed once it is set in motion
c.For what range of m2 will the blocks remain at rest if they are released from rest?
View SolutionBlock B of mass m_(B) = 0.5 kg rests on block A, with mass m_(A) = 1.5kg which in turn is on a horizontal tabletop (as shown in figure) .The coefficient of kinetic friction between block A and the tabletop is mu_(k) = 0.4 and the coefficient of static friction between block A and blockB is mu_(s) = 0.6 A light string attached block A passes over a frictionless, massless pulley and block C is suspeneded from the other end of the string. What is the largest mass m_(c) (in kg) that block C can have so that block A and B still slide together when the system is relaced from rest?
View SolutionTwo blocks A and B are connected by a string as shown as shown in the figure . Friction coefficient of the inclined plane is 0.5 . The mass of the block A is 5 kg. If minimum and maximum values of mass of the block B for which the block A remains in equilibrium are m_(1) and m_(2) then find the value of (m_(2) - m_(1)) [in kg]
View SolutionCoefficient of kinetic friction and coefficient of static friction between two blocks is mu_(k) and mu_(s) respectively. In general
View Solution