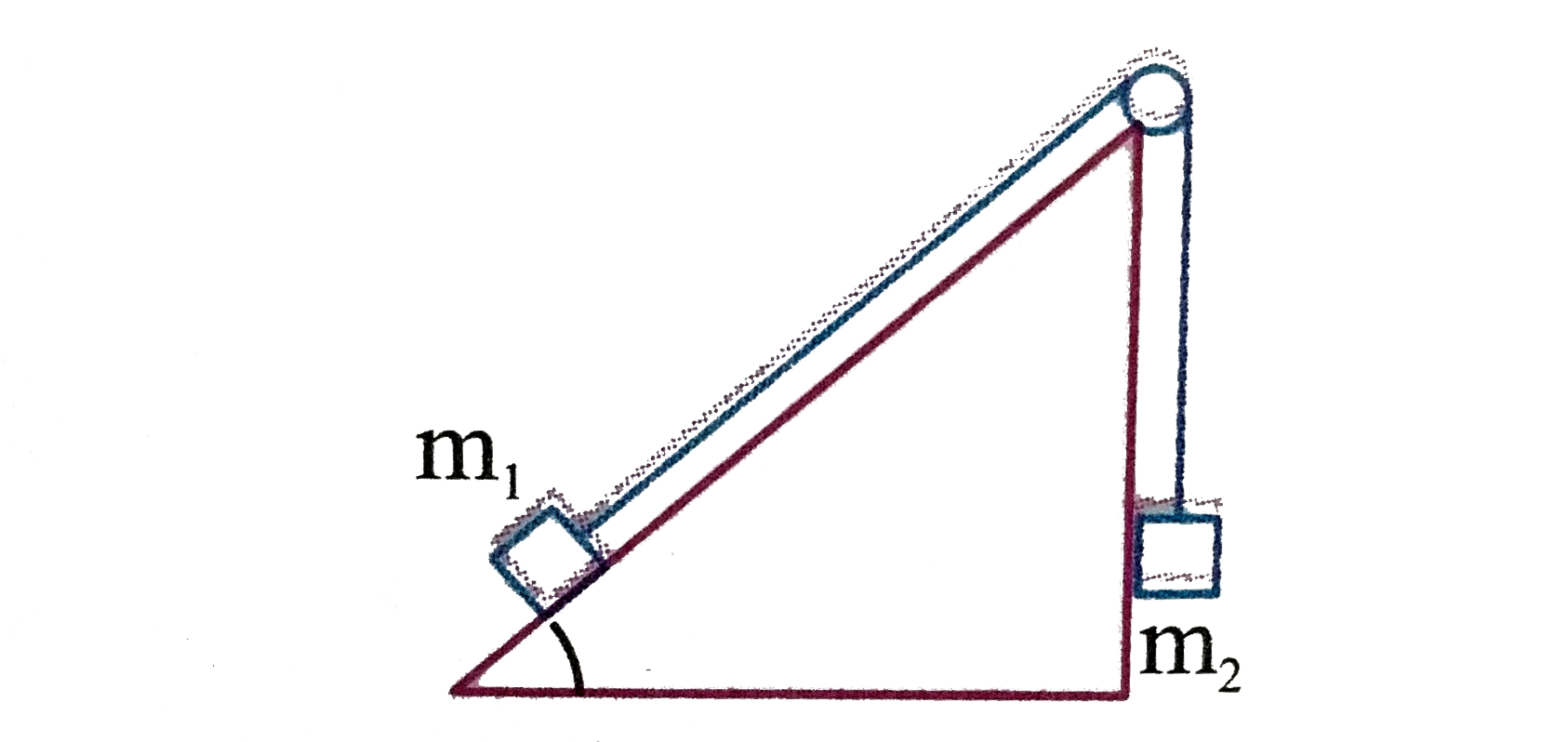
A block with mass m1 is placed on an inclined plane with slope angle α and is connected to a second hunging block with mass m2 by a cord passing over a small . Friction less pulley as shown in fig 7.247 . The coefficient of static friction is μ2 and the coefficient of kinetic friction is μs

a. Find the mass m2 for which block m1 moves up plane at constant speed once it is set in motion
b. Find the mass m2 for which block m1 moves down the plane at constant speed once it is set in motion
c.For what range of m2 will the blocks remain at rest if they are released from rest?
The correct Answer is:m1(sinα+μkcosα)
b.m1(sinα−μkcosα)
c.m1(sinα−μkcosα)<m2<m1(sinα+μscosα)
a. The tension in the cort must be m2g in order that the banging block moves at constant speed .This tension must overcome friction and the component of the gravitational force the incline , so
m2g=(m2gsinα+μkm2gcosα)
and m2=m1(sinα+μkcosα)
b. In this case the friction in the same direction as the tension on the block of mass m1 so ,
m2g=(m1gsinα−μkm2gcosα)
or m2=m1(sinα−μkcosα)
c. similar to the analysis of parts (a) and (b), the largest could be is m1(sinα+μkcosα) and the similar m2 could m1(sinα−μkcosα)
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Single Correct
87 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Multiple Correct
2 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.3
27 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A block of mass m1=2kg on a smooth inclined planeat angle 30∘ is connected to a second block of mass m2=3kg by a cord passing over a frictionless pulley as shown in figure. The acceleration of each block is - (Assume g=10m/sec2 )
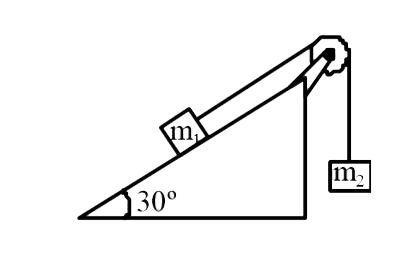
View SolutionCoefficient of kinetic friction and coefficient of static friction between two blocks is μk and μs respectively. In general
View Solution
Knowledge Check
A block of mass M is sliding down the plane. Coefficient of static friction is μs and kinetic friction is μk. Then friction force acting on the block is :
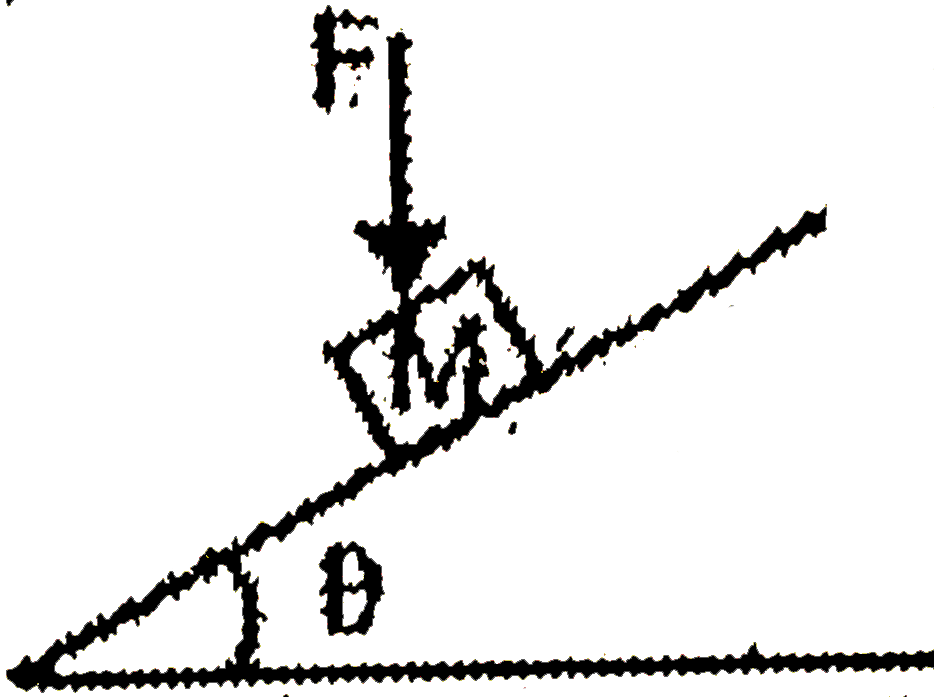 A(F+Mg)sinθBμk(F+Mg)cosθCμsMgcosθD(Mg+F)sinθ
A(F+Mg)sinθBμk(F+Mg)cosθCμsMgcosθD(Mg+F)sinθA block of mass m in the equilib rium on a rough inclined plane with inclination α and coefficient of friction as shown in the figure (μ<tanα). A force F is applied on the block which makes an angle θ with the horizontal as shown in diagram.
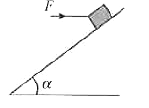 ANormal force on the block mgcosα+Fsinθ.BMinimum force f to keep the blockin equilibrium Fmin=mg(sinα−μcosα)2μ√1+μ2Cμ=tanθDNone of these
ANormal force on the block mgcosα+Fsinθ.BMinimum force f to keep the blockin equilibrium Fmin=mg(sinα−μcosα)2μ√1+μ2Cμ=tanθDNone of theseTwo blocks of masses m1 and m2 are connected by a string of negligible mass which pass over a frictionless pulley fixed on the top of an inclined plane as shown in figure. The coefficient of friction between m1 and plane is μ.
 AIf m1=m2, the mass m1 first begin to move up inclined plane when the angle of inclination θ, then μ=secθ−tanθBIf m1=m2, then mass m1 first begin to side down the plane if μ=secθ−tanθ.CIf m1=2m2, then mass m1 first begins to slide down the plane if μ=2tanθ.DIf m1=2m2, then mass m1 first begins to slide down the plane if μ=tanθ−12secθ.
AIf m1=m2, the mass m1 first begin to move up inclined plane when the angle of inclination θ, then μ=secθ−tanθBIf m1=m2, then mass m1 first begin to side down the plane if μ=secθ−tanθ.CIf m1=2m2, then mass m1 first begins to slide down the plane if μ=2tanθ.DIf m1=2m2, then mass m1 first begins to slide down the plane if μ=tanθ−12secθ.
A block of mass m moves with constant speed down the inclined plane of inclination θ. Find the coefficient of kinetic friction.

View SolutionA cubical block of mass m is sliding on an inclined right angle trough as shown in the figure. If coefficient of friction is μ , find the acceleration of the block.
View SolutionTwo blocks of mass m1 and m2(m2>m1) are placed in contact with each other on an inclined plane as shown in figure . The coefficient of friction between m1 and surface is μ1 and between m2 and surface is μ2.



View SolutionTwo blocks are connected over a massless pulley as shown in figure. The mass of block A is 10 kg and the coefficient of kinetic friction is 0.2 Block A sliders down the incline at constant speed. The mass of block B in kg is

View SolutionA block of mass m is at rest on a rough inclined plane, whose friction coefficient is μ. Net force exerted by surface on block is :-
View Solution
