Two stones are through up simultaneously from the edge of a cliff 240 m high with initial speed of 10 m/s and 40 m/s respectively. Which of the following graphs best represents the time variation of relative position of the second stone with respect to the first? Assume stones do not rebound after hitting the ground and neglect air resistance, take . g=10m/s2 (The figures are schematic and not drawn to scale)
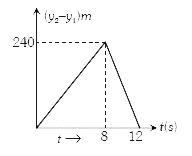


The correct Answer is:C
For the second stone time required to reach the ground is given by
y=ut−12gt2
−240=40t−12×10×t2
(t−12)(t+8)=0
∴T=12s
For the first stone :
−240=10t−12×10×t2
∴−240=10t−5t2
5t2−10t−240=0
(t−8)(t+6)=0
T=8s
During first 8 seconds both the stones are in air :
∴y2−y1=(u2−u1)t=30t
∴ graph of (y2−y1) against t is a straight line
After 8 seconds
y2=u2t−12gt2−240
Stone two has acceleration with respect to stone one .
Similar Questions
Two stones are thrown up simultaneously from the edge of a cliff 200 m high with initial speeds of 15 ms^(-1) and 30 ms^(-1) . Verify that the graph shown in Fig. correctly represents the time variation of the relative position of the second stone with respect to the first. Neglect air resistance and assume that the stones do not rebound after hitting the ground. Take g = 10 ms^(-2) . Give the equations for the linear and curved parts of the plot.
View SolutionTwo stones are thrown up simultaneously from the edge of a cliff 200 m high with initial speeds of 15 ms^(-1) and 30 ms^(-1) . Verify that the graph shown in Fig. correctly represents the time variation of the relative position of the second stone with respect to the first. Neglect air resistance and assume that the stones do not rebound after hitting the ground. Take g = 10 ms^(-2) . Give the equations for the linear and curved parts of the plot.
View SolutionA stone is thrown vertically up from the tower of height 25m with a speed of 20 m/s What time does it take to reach the ground ? (g=10m/s2)
View SolutionTwo stones are thrown up simultaneously from the edge of a cliff 200 m high with initial speeds of 15 ms^(- ) and 30 ms^(-1). Verify that the graph shown in figure. Correctly represents the time variation of the relative position of the second stone with respect to the first. Neglect air resistance and assume that the stones do not rebound after hitting the ground. Take g = 10 ms^(-2). Give the equations for the linear and curved parts of the plot.
View SolutionTwo stones are thrown up simultaneously from the edge of a cliff 200 m high with initial speeds of 15 m s^(-1) and 30 m s^(-1) respectively. The time variation of the relative position of the second stone with respect to the first is shown in the figure. The equation of the linear part is
View SolutionTwo stones are thrown up simultaneously from the edge of a clir 240 m high with initial speed of 10 m/s and 40 m/s respectively. Which of the following graphs best represents the time variation of relative position of the second stone with respect to the first? (Assume stones do not rebound after hitting the ground and neglect air resistance, take g=10 m/s^2 ) (The figures are schematic and not drawn to scale).
View SolutionTwo stones are thrown up simultaneously from the edge of a cliff 240 m high with initial speed of 10 m/s and 40 m/s respectively. Which of the following graph best represents the time variation of relative position of the second stone with respect to the first ?
(Assume stones do not rebound after hitting the ground and neglect air resistance, take g=10ms2) (The figures are schematic and not drawn to scale)
View SolutionTwo stones are thrown up simultaneously from the edge of a cliff 200 m high with initial speeds of 15 ms^(-1) and 30 ms^(-1) . Verify that the graph shown in Fig. correctly represents the time variation of the relative position of the second stone with respect to the first. Neglect air resistance and assume that the stones do not rebound after hitting the ground. Take g = 10 ms^(-2) . Give the equations for the linear and curved parts of the plot.
View Solution