A small block slides without friction down an iclined plane starting form rest. Let Sn be the distance traveled from time t=n−1 to t=n. Then SnSn+1 is:
2n−12n
2n+12n−1
2n−12n+1
2n2n+1
The correct Answer is:C
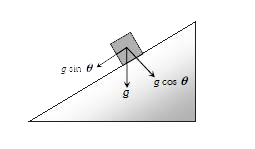
a=gcosθ
Sn=gcosθ2(2n−1)
Sn+1=gcosθ2[2(n+1)−1]
SnSn+1=2n−12n+1
Similar Questions
एक वस्तु एक घर्षणरहित नत समतल पर प्रारम्भिक विरामावस्था से नीचे ओर सरकती है। यदि sn और sn+1 क्रमशः वस्तु द्वारा n वें और (n+1) वें सेकण्ड में चली गई दूरियाँ हो तो sn+1sn अनुपात है
View SolutionA small cube falls from rest along a frictionless inclined plane. If this distance travelled between times t = n -1 and t = n be s_(n) then the value of (s_(n))/(s_(n)+1) is
View SolutionA small block slides without friction down an inclined plane starting from rest. Lets sn be the distance travelled from time t=n - 1 to t = n. Then Snsn+1 is:
View SolutionLet Sn=1+2+3+...+n and Pn=S2S2−1.S3S3−1.S4S4−1...SnSn−1, where n∈N,(n≥2)Thenlimn→∞Pn=__________.
View SolutionA small block slides without friction down an iclined plane starting form rest. Let S_(n) be the distance traveled from time t = n - 1 to t = n . Then (S_(n))/(S_(n + 1)) is:
View SolutionLet Sn,n=1,2,3,… be the sum of infinite geometric series, whose first term is n and the common ratio is 1n+1. Evaluate limn→∞S1Sn+S2Sn−1+S3Sn−2+...+SnS1S21+S22+......+S2n.
View SolutionA particle starts sliding down a frictionless inclined plane. If Sn is the distance travelled by it from time t=n−1sec, to t=nsec, the ratio Snsn+1 is
View SolutionLet S_(n)=1+2+3+...+n " and " P_(n)=(S_(2))/(S_(2)-1).(S_(3))/(S_(3)-1).(S_(4))/(S_(4)-1)...(S_(n))/(S_(n)-1) , where n inN,(nge2) Then underset(ntooo)limP_(n) =__________.
View Solution
