A small block slides without friction down an inclined plane starting from rest. Lets sn be the distance travelled from time t=n - 1 to t = n. Then Snsn+1 is:Solution in Kannada
2n−12n
2n+12n−1
2n−12n+1
2n2n+1
The correct Answer is:c
Here Sn=u+a/2(2n−1)
As u=0
∴Sn=a/2(2n−1)
Also Sn+1=a/2[2n(n+1)−1]=a/2[2n+1]
Hence SnSn+1=2n−12n+1
Topper's Solved these Questions
- DESCRIPTION OF MOTION IN ONE DIMENSION Book:MODERN PUBLICATIONChapter:DESCRIPTION OF MOTION IN ONE DIMENSION Exercise:MULTIPLE CHOICE QUESTION (LEVEL-II)
Explore 54 Videos
- DESCRIPTION OF MOTION IN ONE DIMENSION Book:MODERN PUBLICATIONChapter:DESCRIPTION OF MOTION IN ONE DIMENSION Exercise:Recent Competitive Question
Explore 12 Videos
- CURRENT ELECTRICITYBook:MODERN PUBLICATIONChapter:CURRENT ELECTRICITYExercise:RECENT COMPETITIVE QUESTIONS
Explore 32 Videos
- DESCRIPTION OF MOTION IN TWO AND THREE DIMENSIONBook:MODERN PUBLICATIONChapter:DESCRIPTION OF MOTION IN TWO AND THREE DIMENSIONExercise:Revision TEST
Explore 36 Videos
Similar Questions
A man moves along the path abode as shown in the Fig. What is his displacement from the point of start?
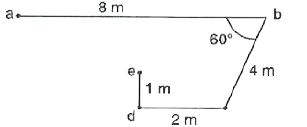
View SolutionA train is moving slowly on a straight track with a constant speed of 2 m s−1 . A passengers in the train starts walking at a stready speed of 2 m s−1 to the back of the train in the opposite direction of the motion of the train. So to an observer standing on the platform directly in front of that passenger, the velocity of the passenger appears to be
View SolutionA battery of emf E has an internal resistance r. A variable resistance R is connected to the terminals of the battery. A current i is drawn from the battery. V is the terminal potential difference. If R alone is gradually reduced to zero, which of the following best describes i and V?
View SolutionThe torque of a force →F=−3ˆi+ˆj+5ˆk acting at a point is →τ. If the position vector of the point vector of the point is 7ˆi+3ˆj+ˆk, then →τ is :
View SolutionThe nth term of an A.P., the sum of whose n terms is Sn , is Sn+Sn−1 (b) Sn−Sn−1 (c) Sn+Sn+1 (d) Sn−Sn+1
View SolutionThe common difference of an A.P., the sum of whose n terms is Sn , is Sn−2Sn−1+Sn−2 (b) Sn−2Sn−1−Sn−2 (c) Sn−Sn−2 (d) Sn−Sn−1
View SolutionA particle starts sliding down a frictionless inclined plane. If Sn is the distance travelled by it from time t=n−1sec, to t=nsec, the ratio Snsn+1 is
View SolutionA small block slides without friction down an iclined plane starting form rest. Let Sn be the distance traveled from time t=n−1 to t=n. Then SnSn+1 is:
View SolutionA small cube falls from rest along a frictionless inclined plane. If this distance travelled between times t = n -1 and t = n be s_(n) then the value of (s_(n))/(s_(n)+1) is
View SolutionIf Sn, denotes the sum of n terms of an A.P., then Sn+3−3Sn+2+3Sn+1−Sn=
View SolutionThe nth term of an A.P., the sum of whose n terms is Sn , is (a)Sn+Sn−1 (b) Sn−Sn−1 (c) Sn+Sn+1 (d) Sn−Sn+1
View SolutionThe common difference of an A.P., the sum of whose n terms is Sn , is (a)Sn−2Sn−1+Sn−2 (b) Sn−2Sn−1−Sn−2 (c) Sn−Sn−2 (d) Sn−Sn−1
View SolutionA small block slides without friction down an iclined plane starting form rest. Let S_(n) be the distance traveled from time t = n - 1 to t = n . Then (S_(n))/(S_(n + 1)) is:
View Solutionif Sn=C0C1+C1C2+...+Cn−1Cn and Sn+1Sn=154 then n is
View SolutionLet Sn denote the sum of first n terms of the sequence 1,5,14,30,55,..... then prove that Sn−Sn−1=∑n2.
View Solution

