A light rod of length 4.0 m is suspended from the ceiling horizontally by means of two vertical wire of equal length tied to its ends. One of the wires is made of steel and is of cross-section 10−3m2 and the other is of brass of cross-section 2×10−3m2. Find out the position along the rod at which a weight may be hung to produce equal stresses in both wires.
1/3
1/4
4/3
1/2
The correct Answer is:D
Since, stress is equal
F1A1=F2A2⇒T1T2=A1A2=0.10.2=12
Similar Questions
A light rod of length 2 m is suspended from the ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of Steel the wires is made of steel and is of cross-section 10−3m2 and the other wire is of brass of cross-section 2×10−3m2. Find out the position along the rod at which a weight may be hung to produce:
(i) equal stress in both wires
(ii) equal strains in both wires
Young.s modulus of brass = 1×1011N/m2
Young.s modulus of steel =2×1011N/m2
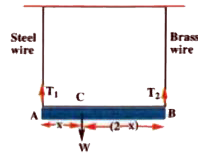
View SolutionA light rod of length 2 m is suspended from ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross-section 0.1 cm sq. and the other of brass of cross-section 0.2 cm sq. Along the rod at what distance a weight may be hung to produce equal stresses in the wires? (Y_("Steel") = 2 xx 10^(11) Nm^(-2), Y_("Bass") = 1 xx 10^(11) Nm^(-2))
View SolutionA light rod of length 2 m is suspended from the ceiling horizontally by mean.s of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross-section 10−3m2 and the other is of brass of cross -section 2×10−3m2. Find out the position along of corss-section 2×10−3m2. Find out the position along the rod at which a weight may be hung to produce, (i) equal stress in both wires (ii) equal strains in both wires
Young.s modulus of brass =1×1011N/m2
Young.s modulus of steel =2×1011N/m2
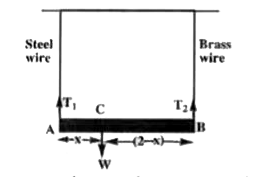
View SolutionA light rod of length 200 cm is suspended from the ceiling horizontally by means of two vertical wires of equal length tied on its end. One of the wires is made of steel and has area of cross-section 0.1cm2 and the order of brass of cross-sectional area 0.2cm2. An object of mass m is hung to the rod. (Ysteel=2×Ybrass)

At which distance from one end of the rod should a weight be hung to produce equal strains in both the wires?
View SolutionA light rod of length of length 2 m is suspended from a ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross - section 10^(-3) m^(2) and the other is of brass of cross- section 2xx10^(-3) m^(2).x is the distance from the steel wire end, at which a weight may be hung. Y_(steel) = 2xx10^(11) Pa and Y_(brass) = 10^(11) Pa Which of the following statement(s) is /are correct ?
View SolutionA light rod of length of length 2m is suspended from a ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross - section 10−3m2 and the other is of brass of cross- section 2×10−3m2.x is the distance from the steel wire end, at which a weight may be hung. Ysteel=2×1011PaandYbrass=1011Pa
Which of the following statement(s) is /are correct ?
View SolutionA light rod of length 2 m is suspended from the ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross section 0.1 cm^(2) . The other wire is a brass of cross section 0.2 cm^(2) . A weight is suspended from a certain point of the rod such that equal stress are produced in both the wires. Which of the following are correct?
View SolutionA light rod of length 200cm is suspended from the ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is cross-section 0.1cm^(2) and the other of brass of cross-section 0.2cm^(2) . Along the rod at which distance may a weight be hung to produce (a) equal stresses in both the wires (b) equal strains in both the wires ? Y or brass and steel are 10xx10^(11) and 20xx10^(11)"dyne"//cm^(2) respectively.
View Solution