A light rod of length 2m is suspended from the ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross section 0.1cm2. The other wire is a brass of cross section 0.2cm2. A weight is suspended from a certain point of the rod such that equal stress are produced in both the wires. Which of the following are correct?
The ratio of tension in the steel and brass wires is 0.5
The load is suspended at a distance of 400/3 cm from the steel wire.
Both (a) and (b) are correct
Neither (a) nor b) is correct.
The correct Answer is:A, B, C
To solve the problem step by step, we will analyze the situation involving the light rod suspended by two wires made of different materials (steel and brass) and determine the conditions for equal stress and the position of the suspended weight.
Step 1: Understand the Setup
We have a light rod of length L=2m suspended horizontally from the ceiling. It is held by two vertical wires: one made of steel with a cross-sectional area As=0.1cm2 and the other made of brass with a cross-sectional area Ab=0.2cm2.
Step 2: Equal Stress Condition
According to the problem, the stresses in both wires are equal. Stress (σ) is defined as:
σ=FA
where F is the force in the wire and A is the cross-sectional area.
For the steel wire:
σs=FsAs
For the brass wire:
σb=FbAb
Setting these equal gives:
FsAs=FbAb
Step 3: Calculate the Ratio of Forces
From the above equation, we can express the ratio of the forces:
FsFb=AsAb
Substituting the given areas:
FsFb=0.1cm20.2cm2=12
This means:
Fs=12Fb
Step 4: Rotational Equilibrium
To find the position of the weight suspended from the rod, we need to consider rotational equilibrium about the point of application of the load. Let the distance from the steel wire to the load be x and from the brass wire to the load be L−x.
The condition for rotational equilibrium is:
Fs⋅x=Fb⋅(L−x)
Step 5: Substitute the Force Ratio
Substituting Fs=12Fb into the equilibrium equation:
(12Fb)⋅x=Fb⋅(L−x)
Dividing both sides by Fb (assuming Fb≠0):
12x=L−x
Step 6: Solve for x
Rearranging gives:
12x+x=L
32x=L
x=23L
Substituting L=2m:
x=23⋅2=43m=400cm
Conclusion
The weight is suspended at a distance of 4003cm from the steel wire.
Summary of Correct Options
1. The ratio of the forces in the wires is Fs:Fb=1:2.
2. The distance from the steel wire to the load is 4003cm.
3. Therefore, both statements A and B are correct.
Final Answer
The correct options are:
- Option 1: Correct
- Option 2: Correct
- Option 3: Both A and B are correct
- Option 4: Incorrect
We have a light rod of length L=2m suspended horizontally from the ceiling. It is held by two vertical wires: one made of steel with a cross-sectional area As=0.1cm2 and the other made of brass with a cross-sectional area Ab=0.2cm2.
According to the problem, the stresses in both wires are equal. Stress (σ) is defined as:
σ=FA
where F is the force in the wire and A is the cross-sectional area.
σs=FsAs
For the brass wire:
σb=FbAb
Setting these equal gives:
FsAs=FbAb
From the above equation, we can express the ratio of the forces:
FsFb=AsAb
Substituting the given areas:
FsFb=0.1cm20.2cm2=12
This means:
Fs=12Fb
To find the position of the weight suspended from the rod, we need to consider rotational equilibrium about the point of application of the load. Let the distance from the steel wire to the load be x and from the brass wire to the load be L−x.
Fs⋅x=Fb⋅(L−x)
Substituting Fs=12Fb into the equilibrium equation:
(12Fb)⋅x=Fb⋅(L−x)
Dividing both sides by Fb (assuming Fb≠0):
12x=L−x
Rearranging gives:
12x+x=L
32x=L
x=23L
Substituting L=2m:
x=23⋅2=43m=400cm
The weight is suspended at a distance of 4003cm from the steel wire.
1. The ratio of the forces in the wires is Fs:Fb=1:2.
2. The distance from the steel wire to the load is 4003cm.
3. Therefore, both statements A and B are correct.
The correct options are:
- Option 1: Correct
- Option 2: Correct
- Option 3: Both A and B are correct
- Option 4: Incorrect
Topper's Solved these Questions
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Assertion- Reasoning
13 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Linked Comprehension
30 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Single Correct
112 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
Similar Questions
A light rod AC of length 2.00 m is suspended from the ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross-section 10−3m2 and the other is of brass of cross-section 2×10−3m2. The position of point D from end A along the rod at which a weight may be hung to produce equal stress in both the wires is [Young's modulus of steel is 2×1011Nm2 and for brass is 1×1011Nm−2]

View SolutionA light rod of length of length 2m is suspended from a ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross - section 10−3m2 and the other is of brass of cross- section 2×10−3m2.x is the distance from the steel wire end, at which a weight may be hung. Ysteel=2×1011PaandYbrass=1011Pa
Which of the following statement(s) is /are correct ?
View Solution
Knowledge Check
A light rod of length 2 m is suspended from ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross-section 0.1 cm sq. and the other of brass of cross-section 0.2 cm sq. Along the rod at what distance a weight may be hung to produce equal stresses in the wires?
(YSteel=2×1011Nm−2,YBass=1×1011Nm−2)A43m from steel wireB43m from brass wireC1 m from steel wireD14m from brass wire
A light rod of length of length 2m is suspended from a ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross - section 10−3m2 and the other is of brass of cross- section 2×10−3m2.x is the distance from the steel wire end, at which a weight may be hung. Ysteel=2×1011PaandYbrass=1011Pa
Which of the following statement(s) is /are correct ?
View SolutionA light rod of length L=2m is suspended horizontally from the ceiling by two wires A and B of equal lengths. The wire A is made of steel with the area of cross section AS=1×10−5m2, while the wire B is made of brass of cross sectional area Ab=2×10−5m2. A weight W is suspended at a distance x from the wire A as shown in figure.
Take, Young's modulus of steel and brass as Ys=2×1011Nm−2 and Yb=1×1011Nm−2.
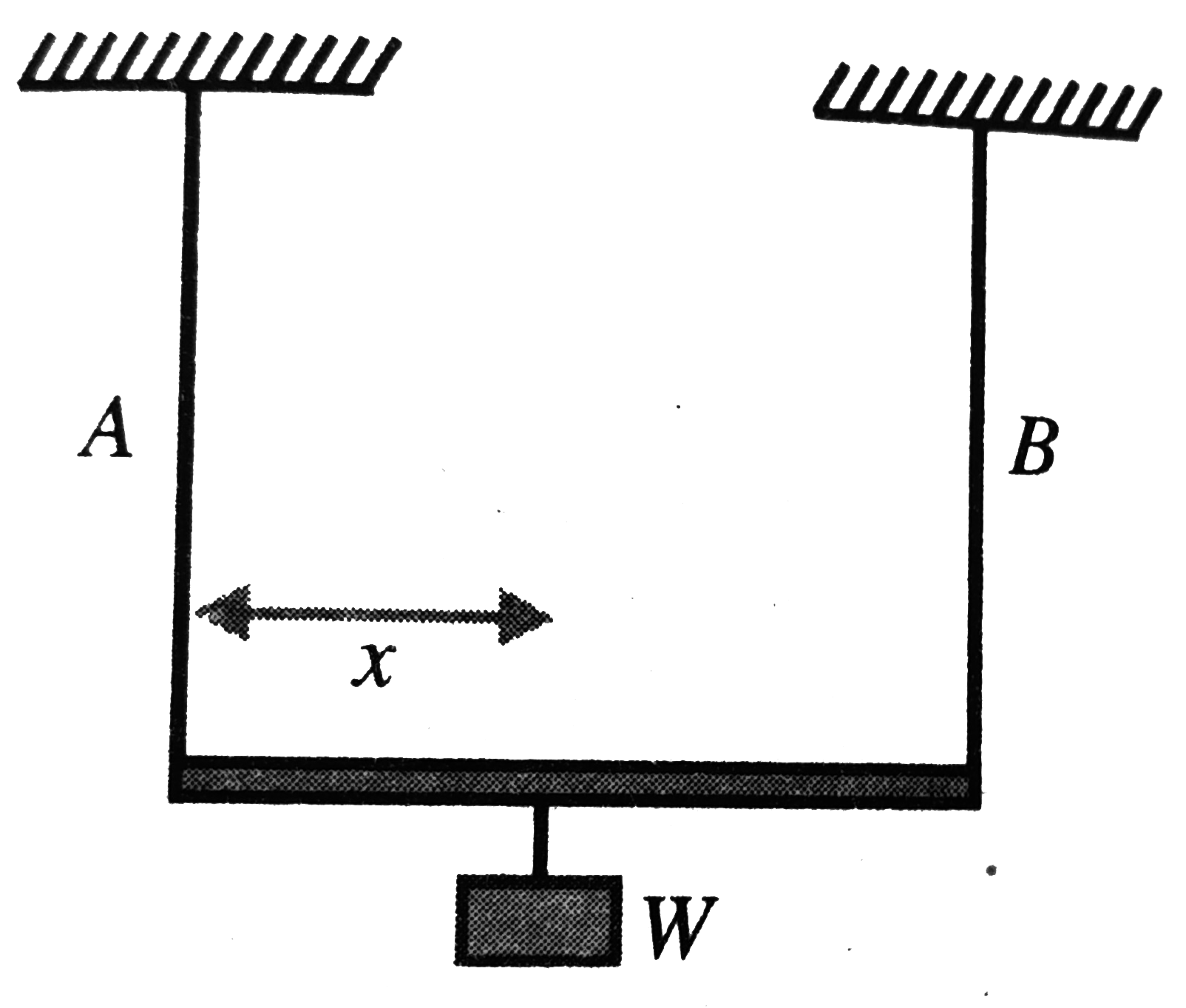
Determine the value of x so that equal stresses are produced in each wire.
View SolutionA light rod of length L=2m is suspended horizontally from the ceiling by two wires A and B of equal lengths. The wire A is made of steel with the area of cross section AS=1×10−5m2, while the wire B is made of brass of cross sectional area Ab=2×10−5m2. A weight W is suspended at a distance x from the wire A as shown in figure.
Take, Young's modulus of steel and brass as Ys=2×1011Nm−2 and Yb=1×1011Nm−2.
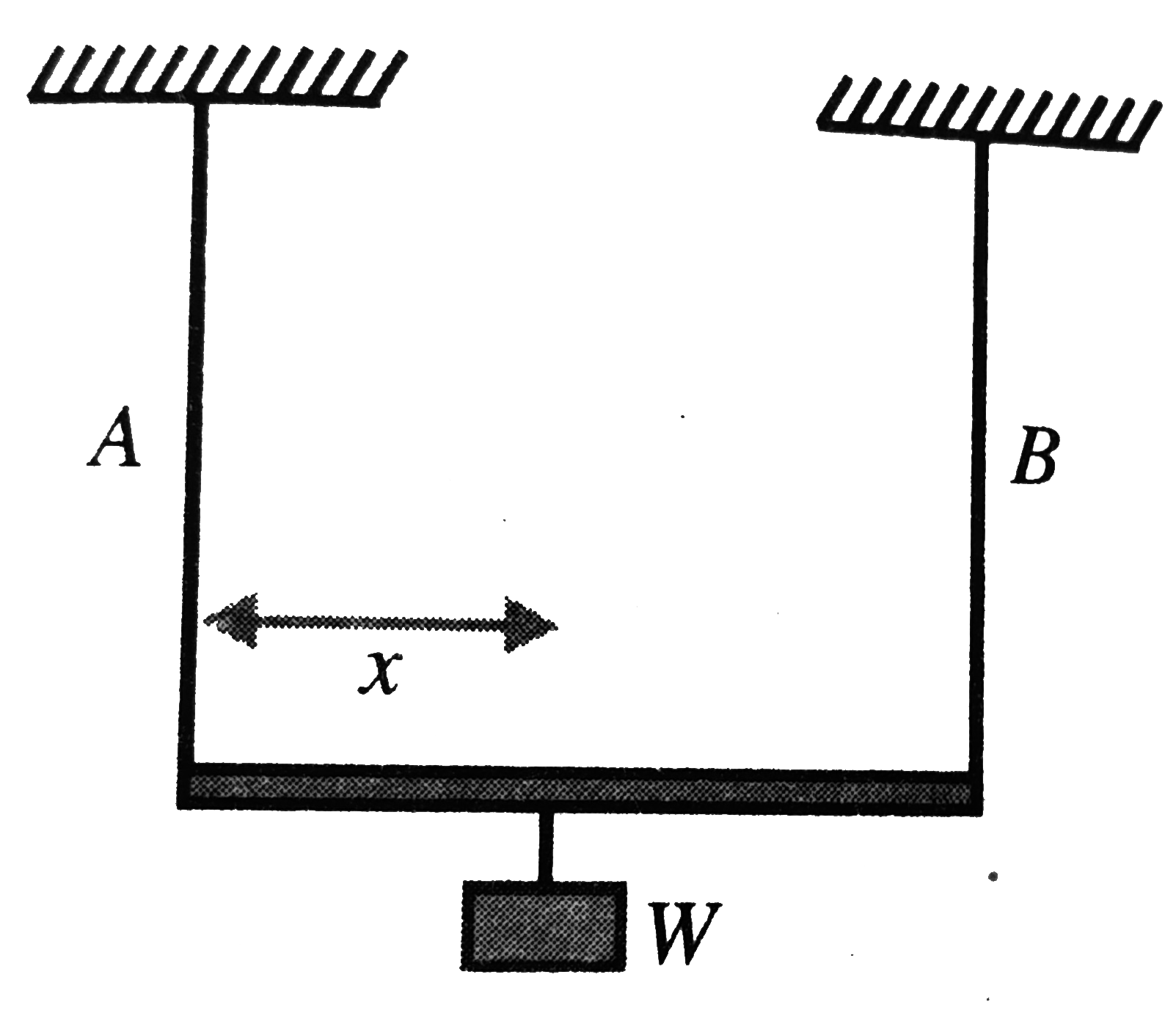
Determine the value of x so that equal strains are produced in each wire
View SolutionA 2 m long light metal rod AB is suspened form the c eiling horizontally by means of two vertices wires of equal length, tied to the ends. One brass and has corss section of 0.3×10−4m2 and the other is of steel with 0.1×10−4m2 corss-section. In order to have equal stresses in the two wires, a weight is hung from the rod. The position of weight along the rod from end A should be.
View SolutionA steel wire 2m long is suspended from the ceiling. When a mass is hung from its lower end, the increase in length recorded is 1cm. Determine the strain in the wire.
View SolutionAn iron rod B of length 1 m and mass 1 kg is suspended with help of two wires as shwon in figure. The area of cross-section of iron wire is 0.3 cm2 and of copper wire is 0.6cm2.
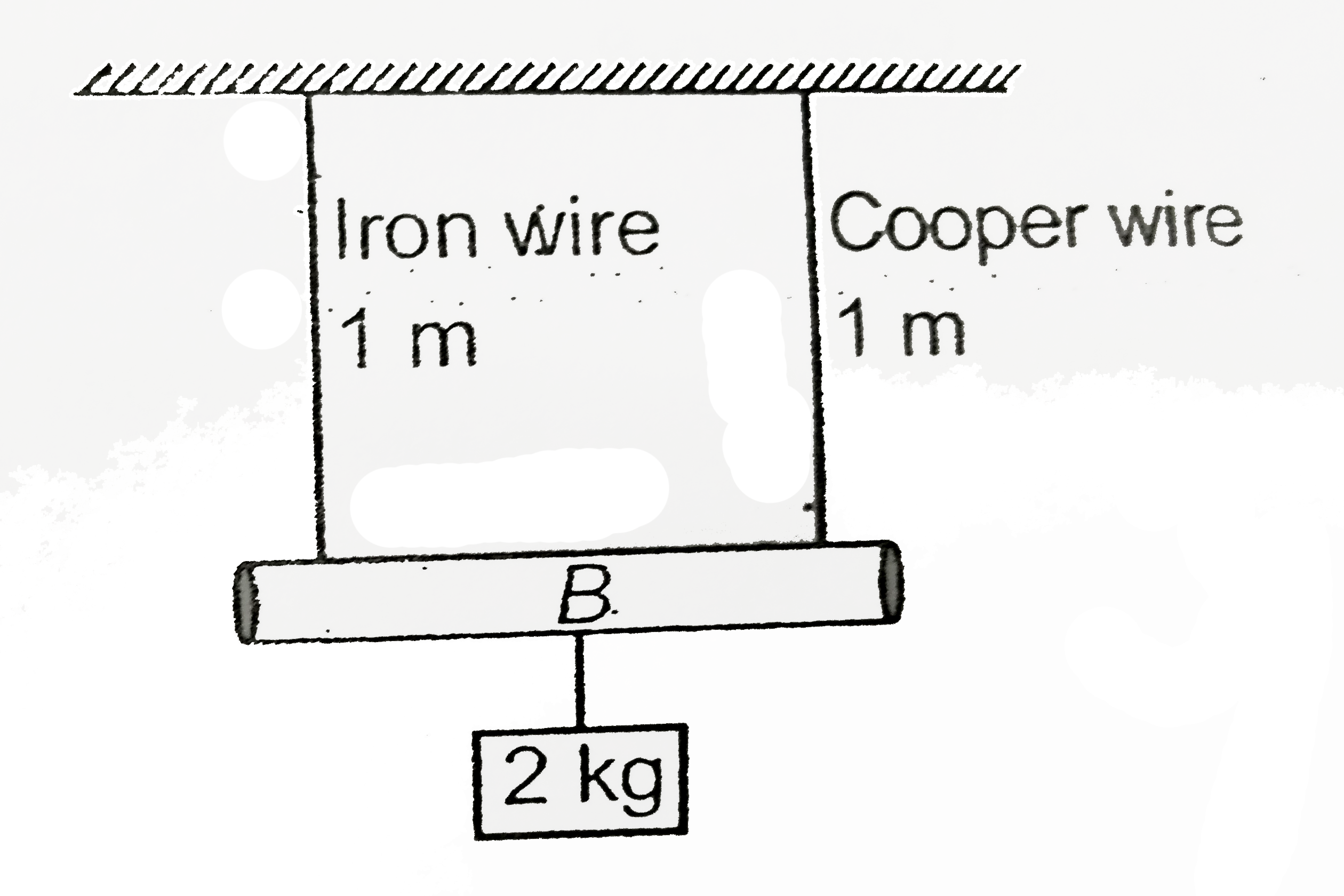
At what distance from iron wire a weight can be hung to produce equal stress in wires?
View SolutionA uniform steel rod of cross- sectional area A and L is suspended so that it hangs vertically. The stress at the middle point of the rod is
View Solution
