Two moasses m1=5kgandm2=10kg, connected by an inextensible string over a frictionless pulley, are moving as shown in the figure. The coefficient of friction of horizontal surface is 0.15. The minimum weitght m that should be put on top of m2 to stop the motion is :-
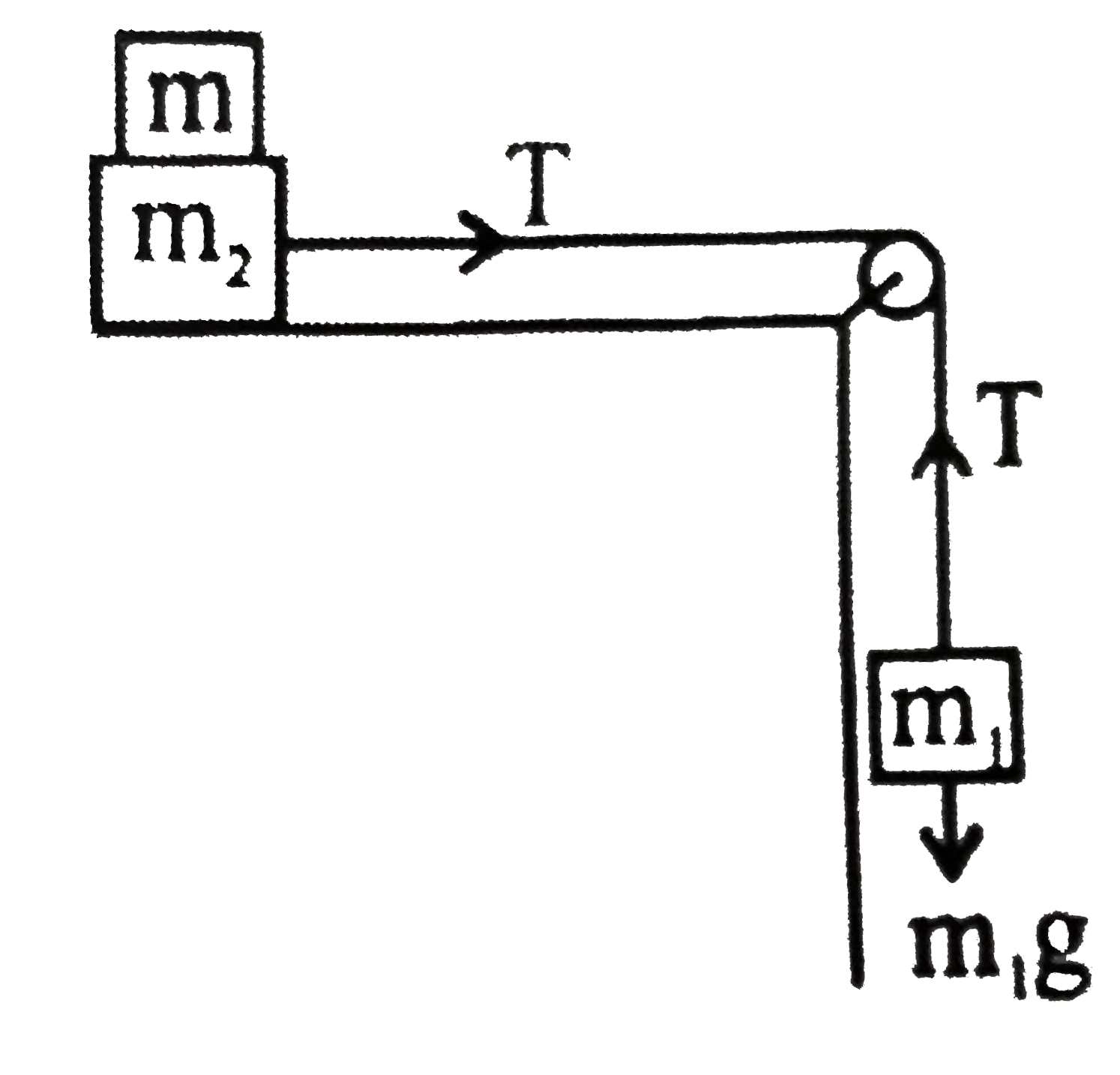
43.3 kg
10.3 kg
18.3 kg
27.3 kg
The correct Answer is:D
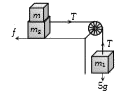
For keeping m1 to be at rest
T = 5g
and for m and m2 to be at rest.
f=T=5g
f≤μN
⇒f≤0.15(m+m2)g⇒50≤15(m+10)10
⇒m≥23.33 kg
Similar Questions
Find the relation between acceleration of the two blocks m_(1) and m_(2) . Assume pulleys are massless and frictionless and the strings are inextensible .
View SolutionTwo masses m1 = 5 kg and m2 = 10 kg, connected by an inextensible string over a frictionless pulley are moving as shown in the figure. The coefficient of friction of horiztonal surface is 0.15. The minimum height m that should be put on top of m2 to stop the motion is
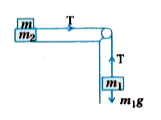
View SolutionTwo masses m_(1)=5kg and m_(2)=10kg, connected by an inextensible string over a frictionless pulley, are moving as shown in the figure. The coefficient of friction of horizontal surface is 0.15. The minimum weitght m that should be put on top of m_(2) to stop the motion is :-
View SolutionTwo masses m1kg and m2kg passes over a pulley. Find the ratio of the masses m1andm2 so that string passes over the pulley will just start slipping over is surface. The friction coefficient between the string and pulley surface is 0.2
View SolutionTwo masses m1kg and m2kg passes over a pulley. Find the ratio of the masses m1andm2 so that string passes over the pulley will just start slipping over is surface. The friction coefficient between the string and pulley surface is 0.2
View SolutionTwo moasses m1=5kgandm2=10kg, connected by an inextensible string over a frictionless pulley, are moving as shown in the figure. The coefficient of friction of horizontal surface is 0.15. The minimum weitght m that should be put on top of m2 to stop the motion is :-

View SolutionA system consists of three masses m1 , m1 , m1 , m2 and m3 connected by a string passing over a pulley P . The mass m1 hangs freely and m2 and m3 are on a rough horizontal table (the coefficient of friction=mu) The pulley is frictionless and of negligible mass. The downward acceleration of m1 is (Assume m1=m2=m3=m).

View SolutionThree blocks of masses m1,m2 and M are arranged as shown in figure. All the surfaces are fricationless and string is inextensible. Pulleys are light. A constant force F is applied on block of mass m1. Pulleys and string are light. Part of the string connecting both pulleys is vertical and part of the strings connecting pulleys with masses m1 and m2 are horizontal.
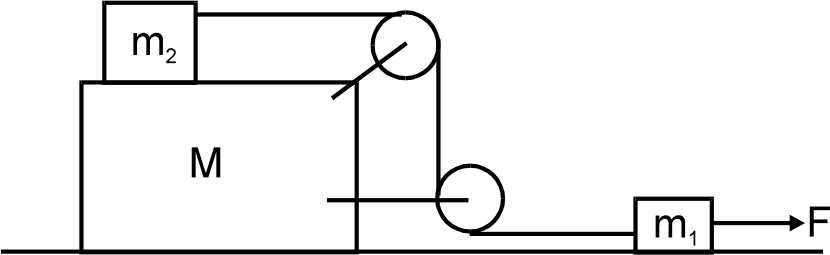
(P)Accleration of mass m1(1)Fm1(Q)Acceleration of massm2(2)Fm1+m2(R)Acceleration of mass M(3)zero(S)Tension in the string(4)m2Fm1+m2
View Solution
